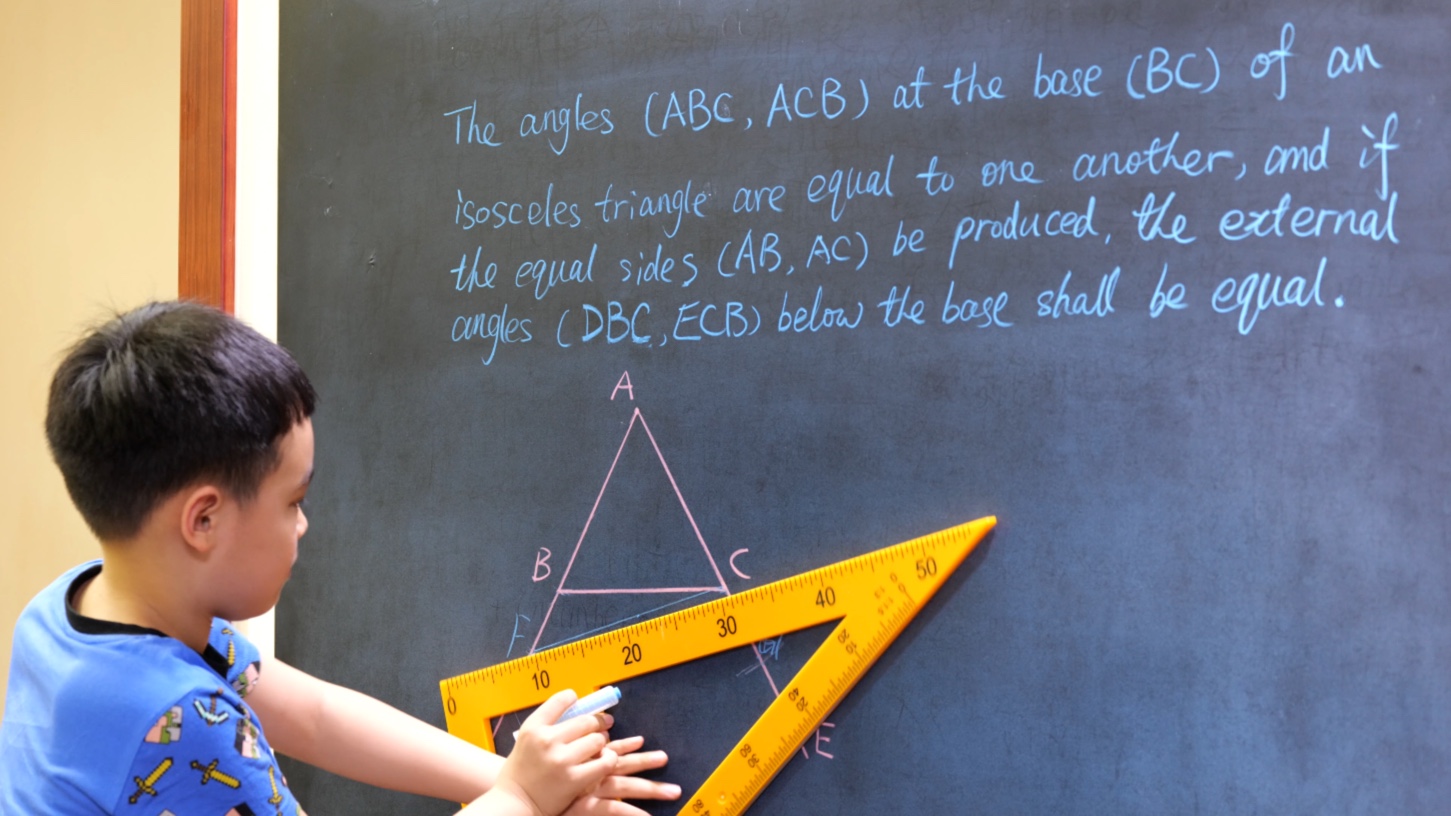Mr. Eric

Euclid Book I PROP. V. – THEOREM.

The angles $(\angle ABC, \angle ACB)$ at the base $(BC)$ of an isosceles triangle are equal to one another, and if the equal sides $(AB, AC)$ be produced, the external angles $(\angle DBC, \angle ECB)$ below the base shall be equal.

Euclid Book I PROP. IV. – THEOREM.

If two triangle $(\triangle BAC, \triangle EDF)$ have two sides $(BA, AC)$ of one equal respectively to two sides

Euclid Book I PROP. III. – PROBLEM.

From the greater $(AB)$ of two given right lines to cut off a part equal to $(C)$ the less.

Euclid Book I PROP. II. – PROBLEM.

From a given point $(A)$ to draw a right line equal to a given finite right line $(BC)$.

Euclid Book I PROP. I. – PROBLEM.

On a given finite right line $(AB)$ to construct an equilateral triangl.