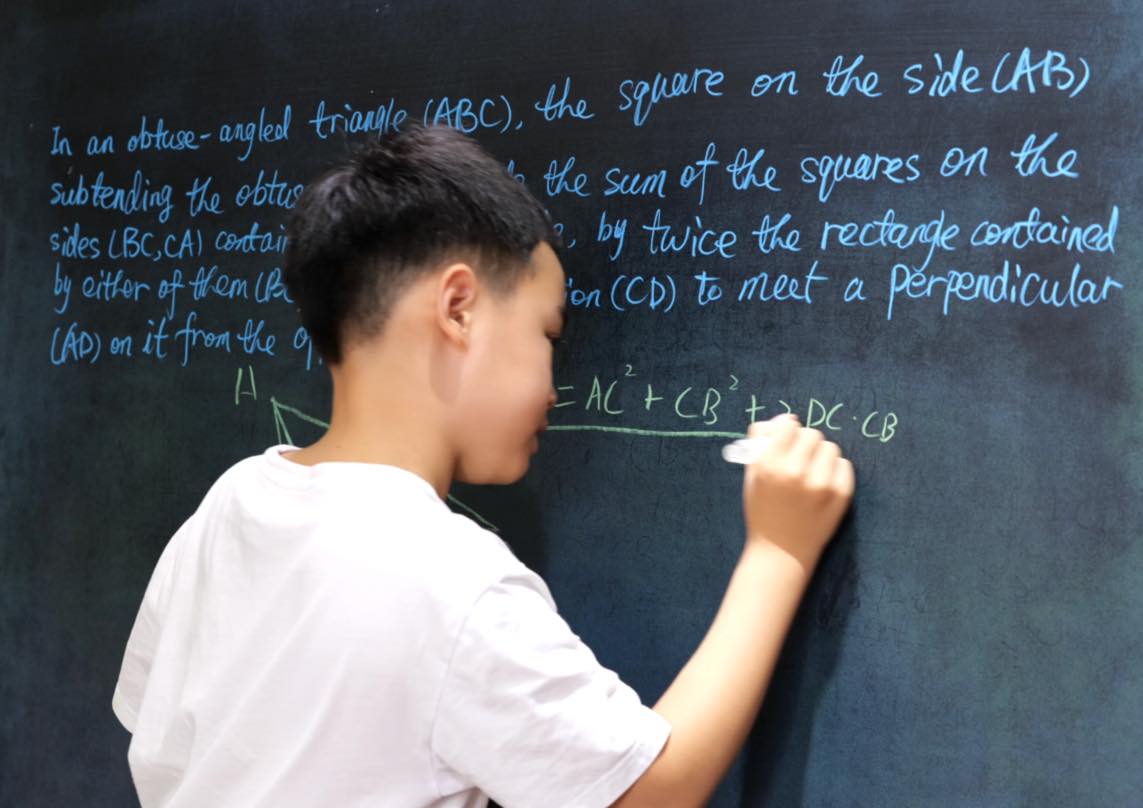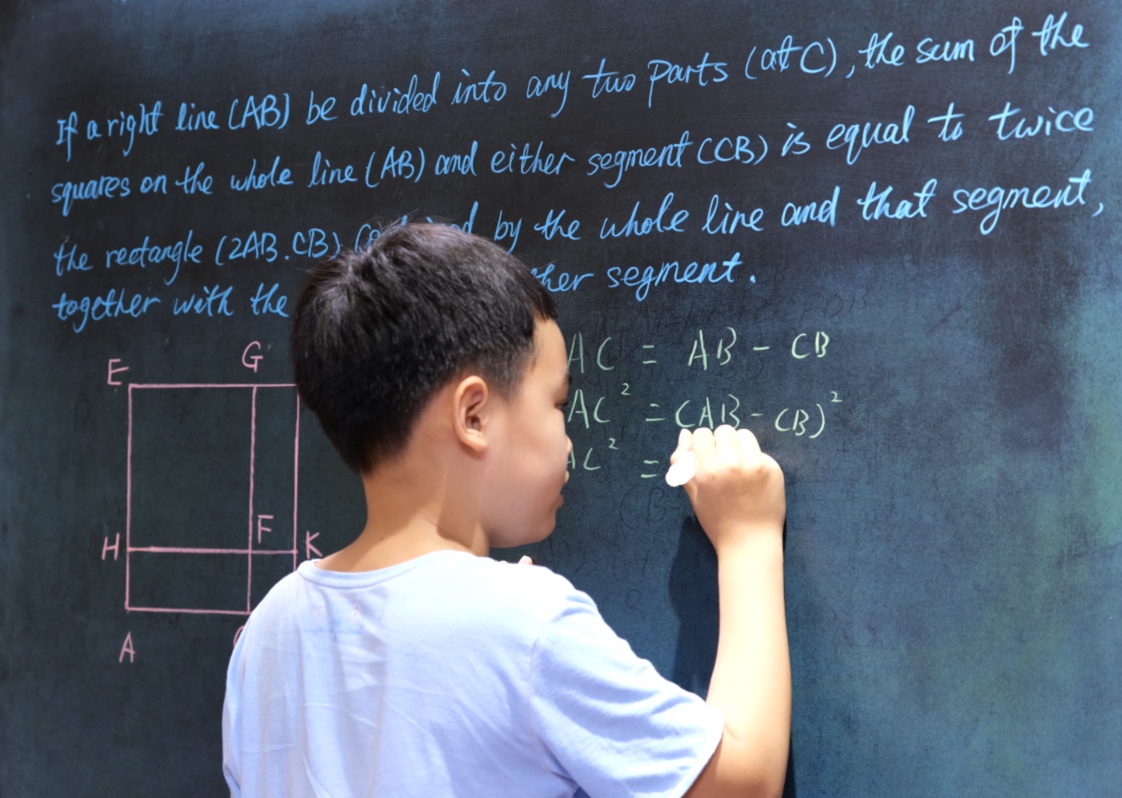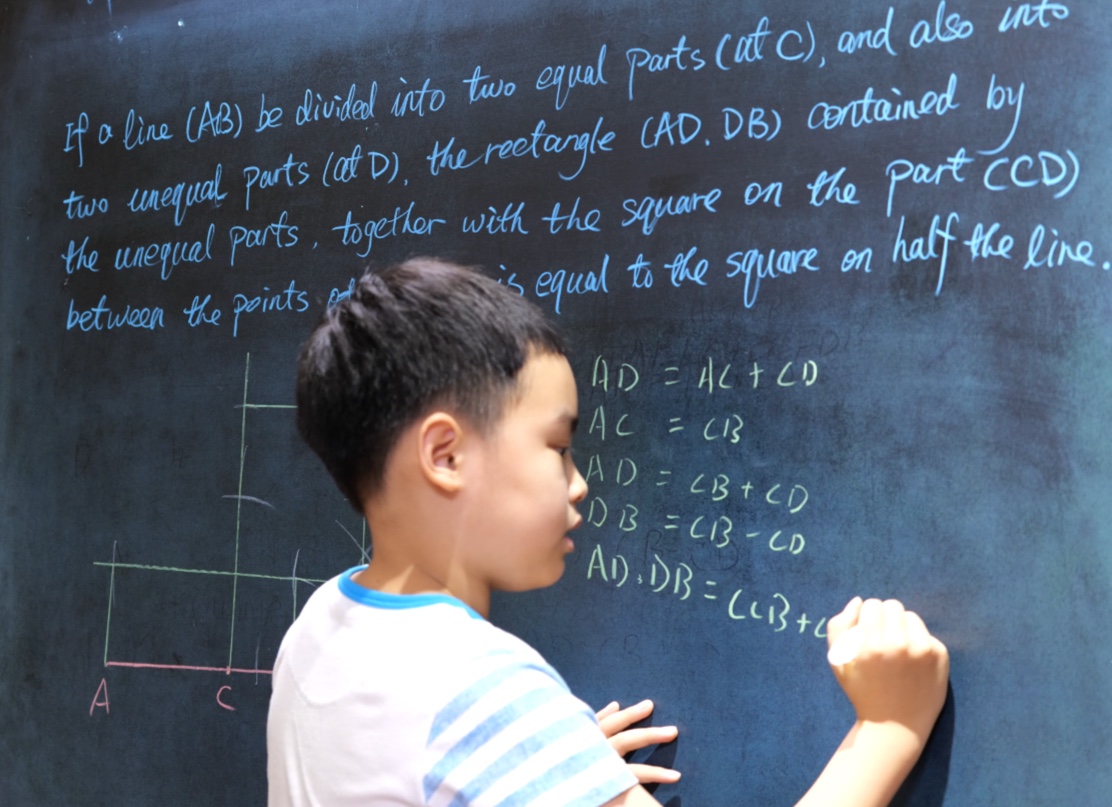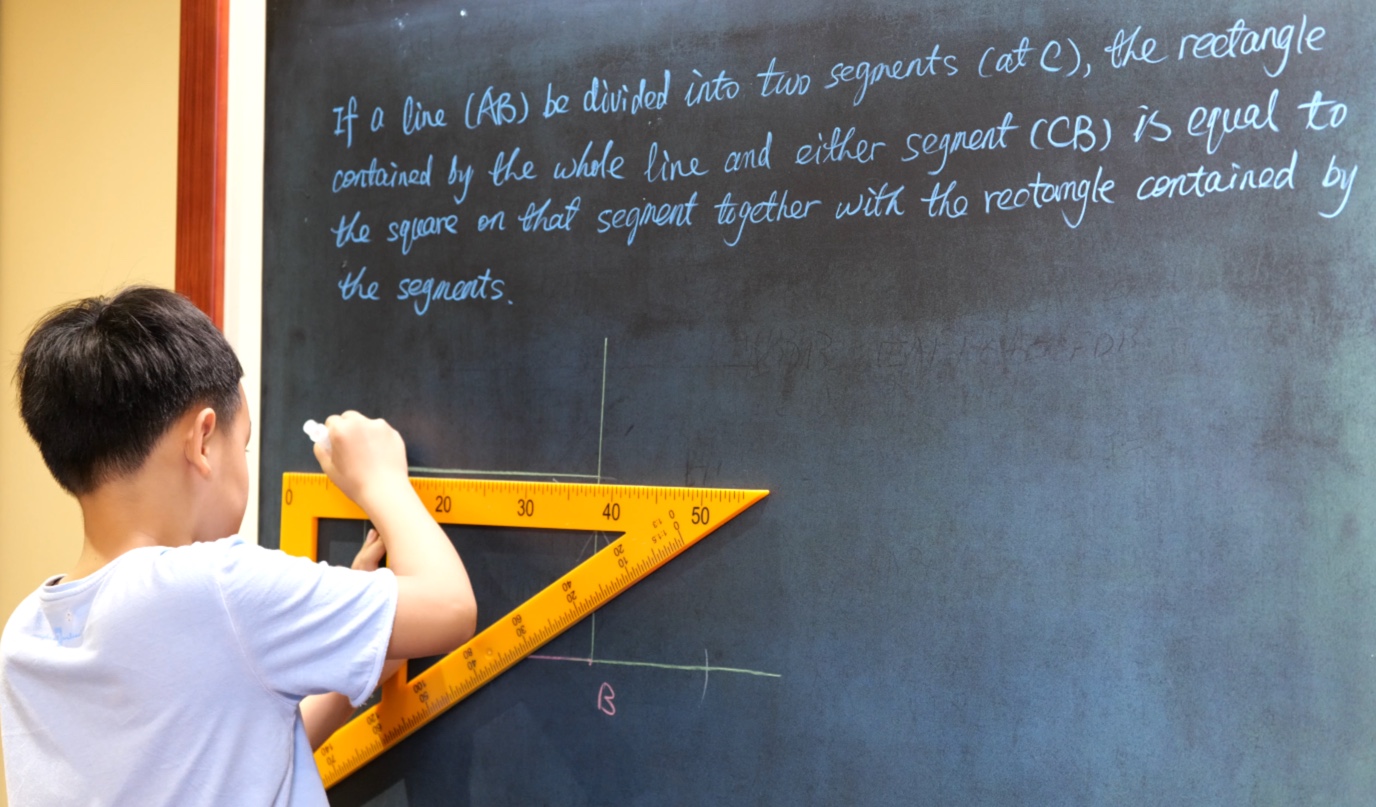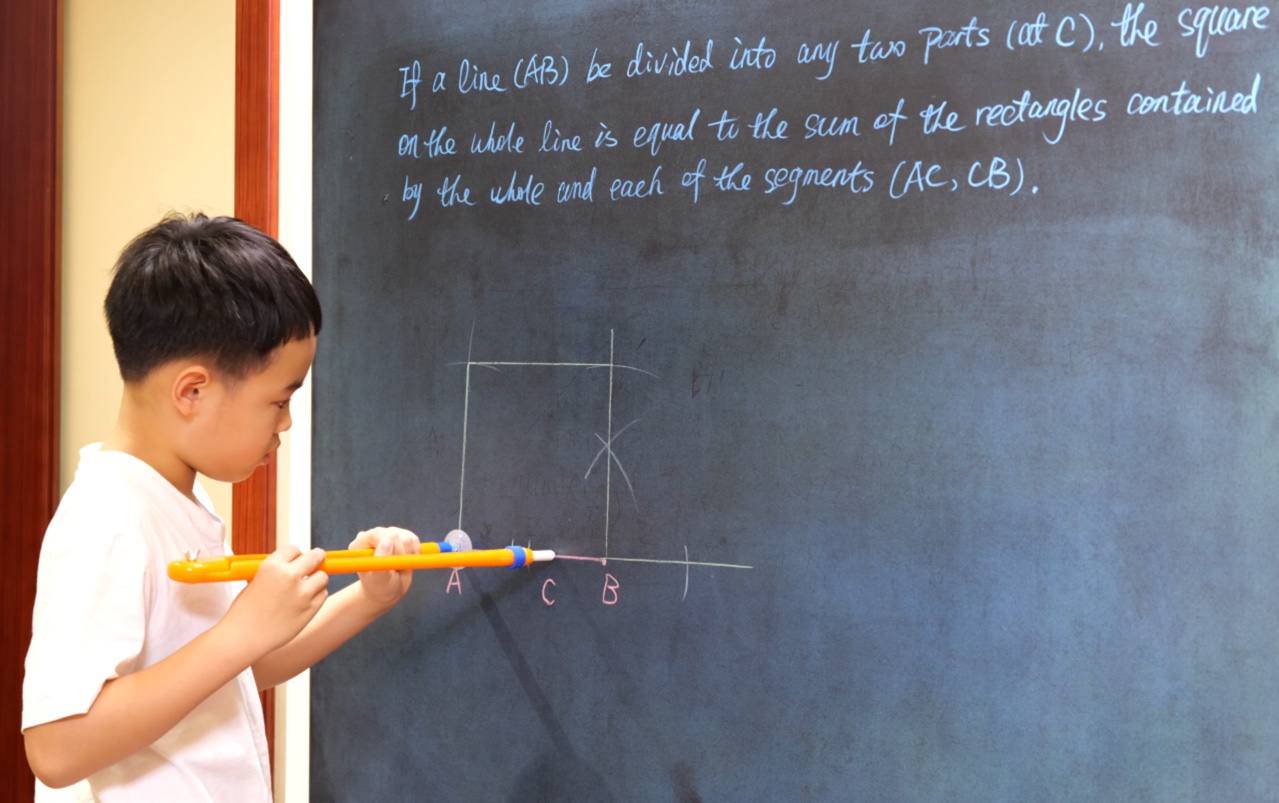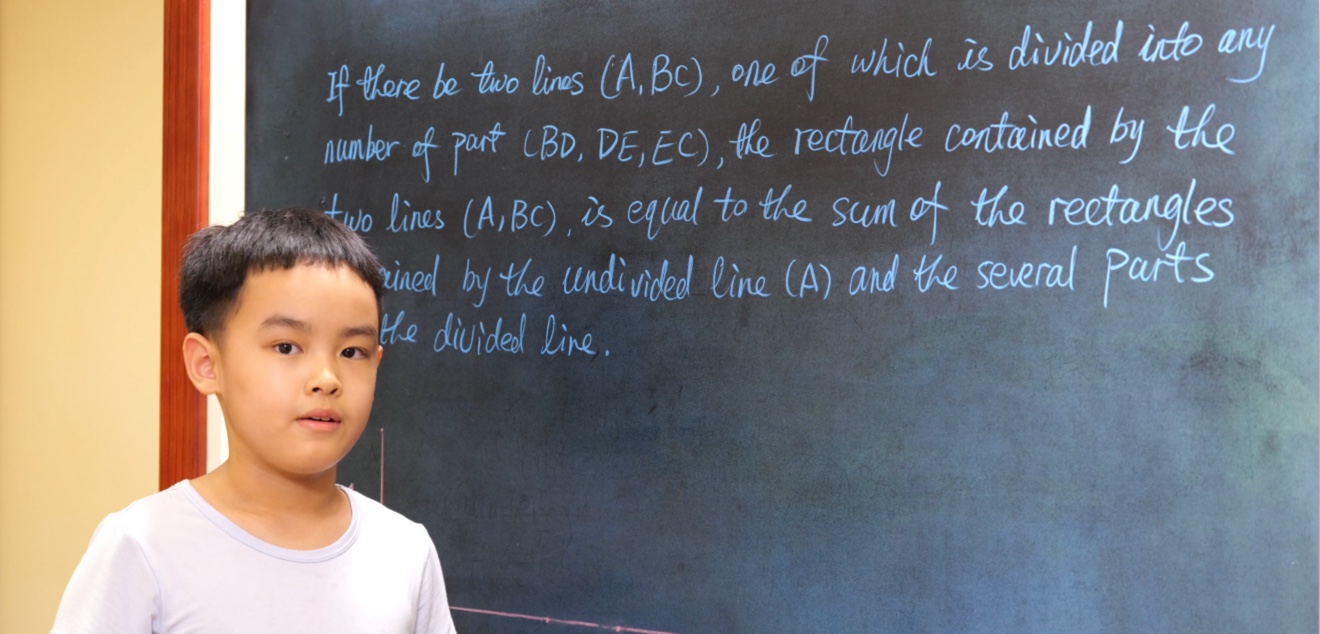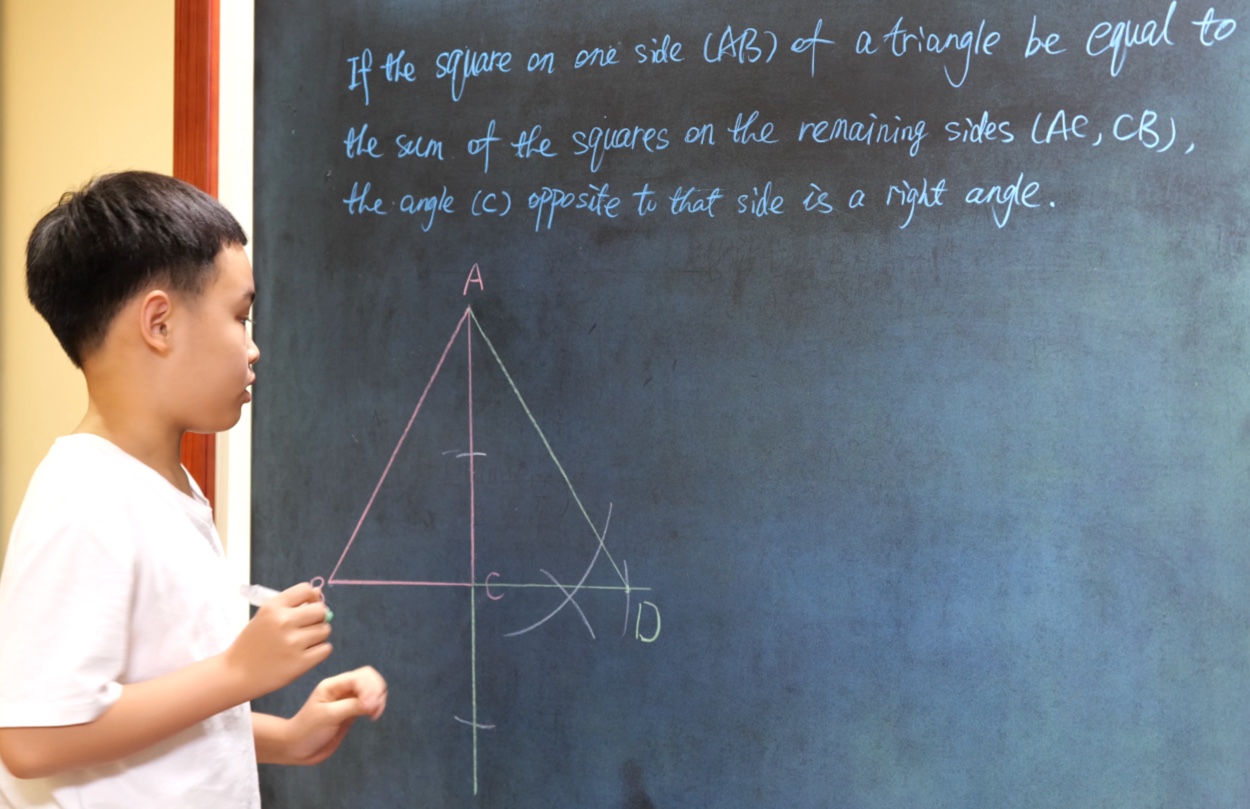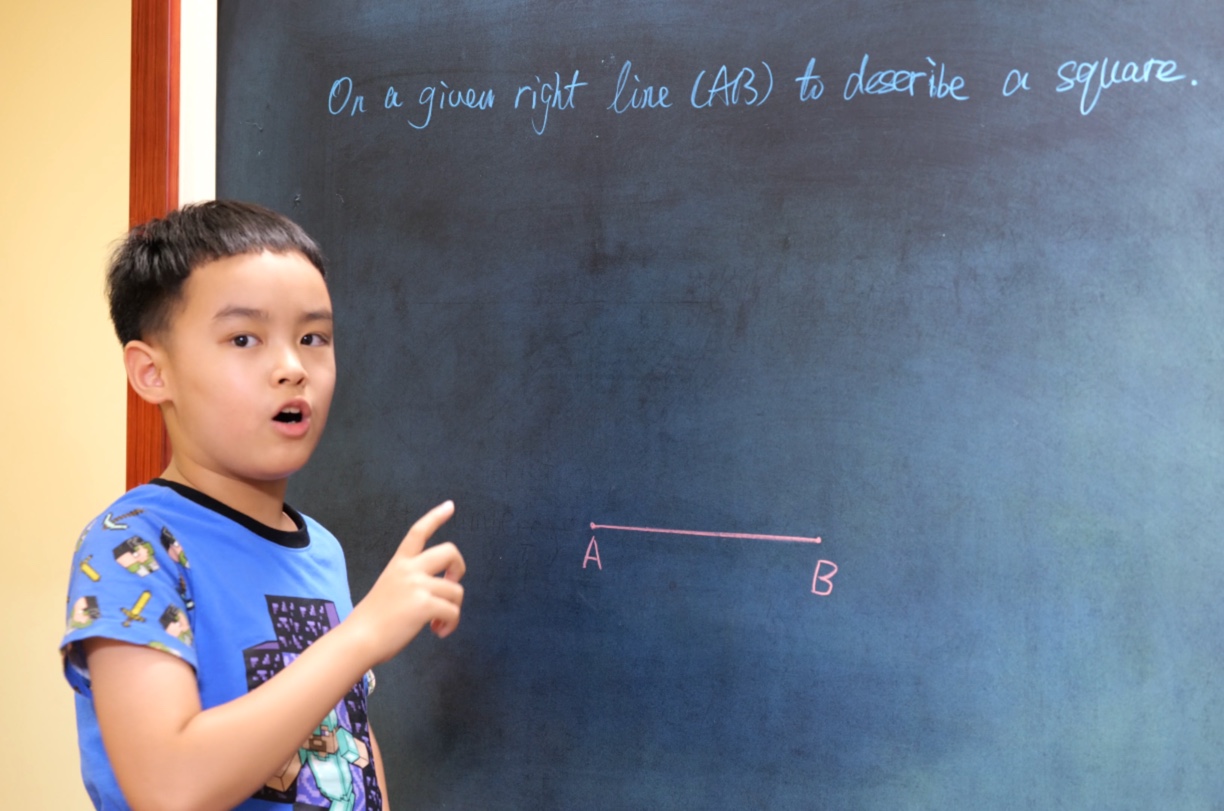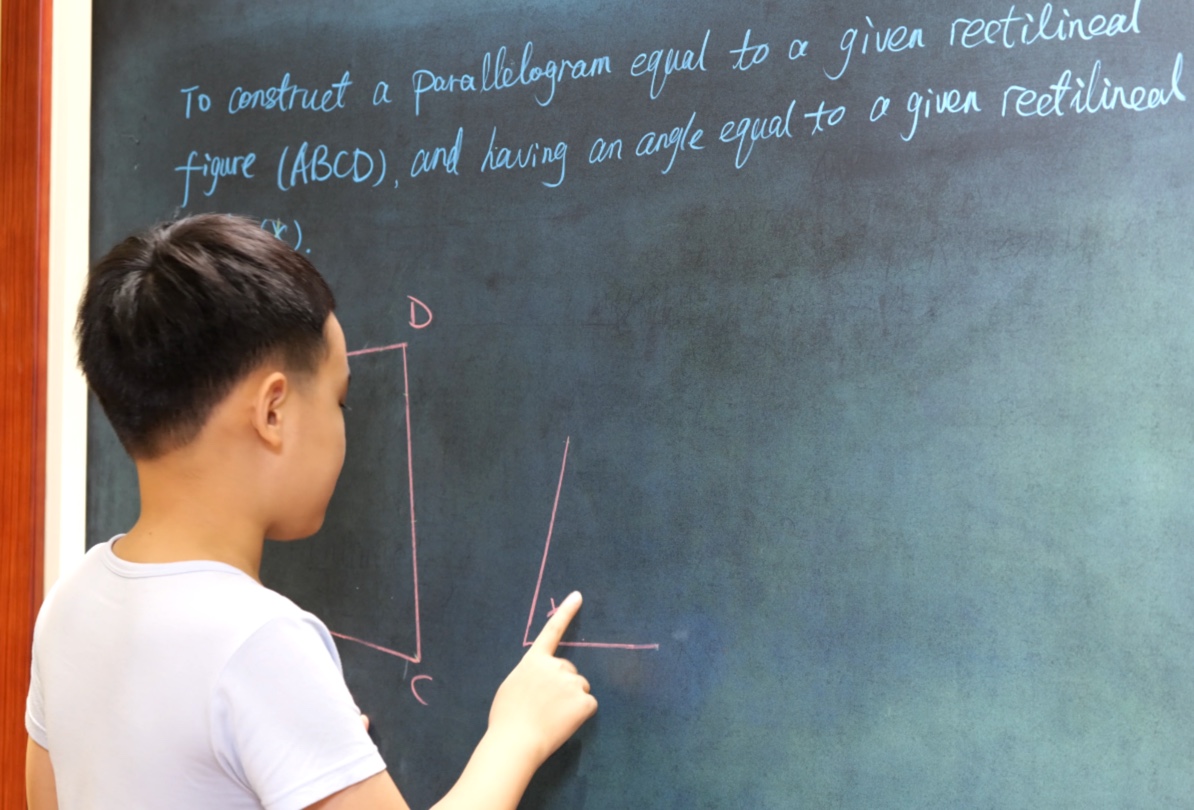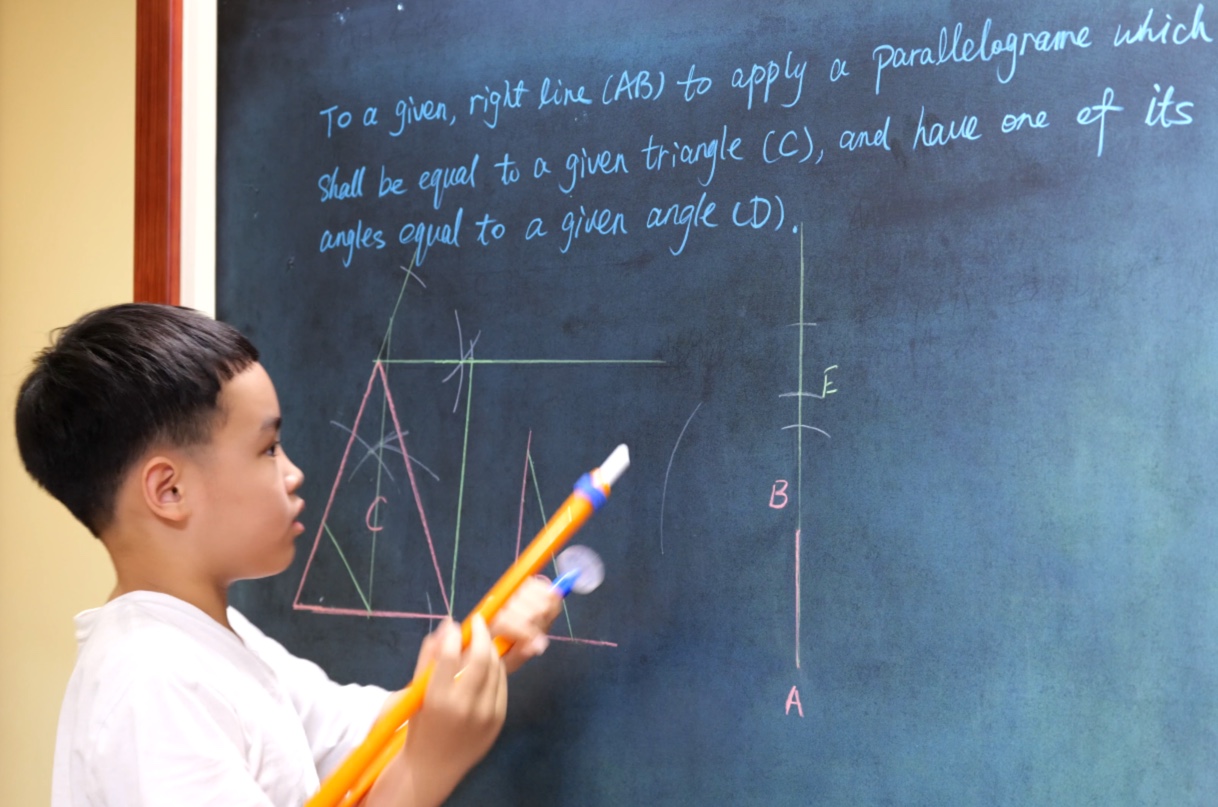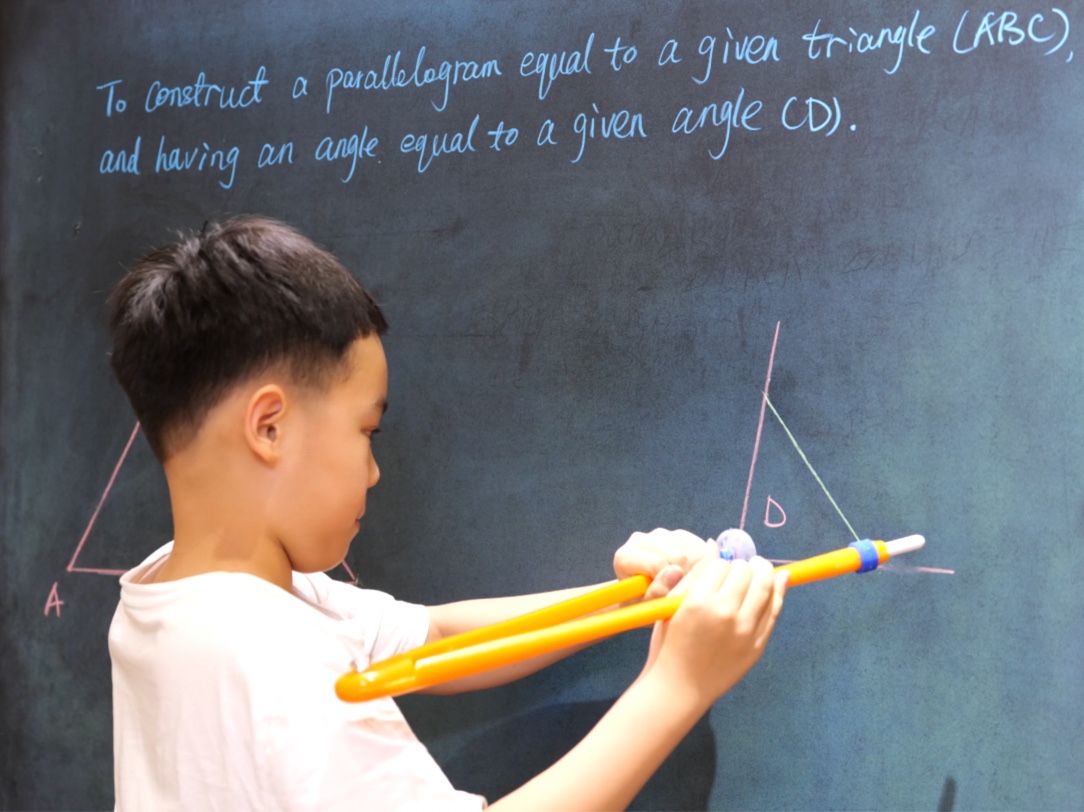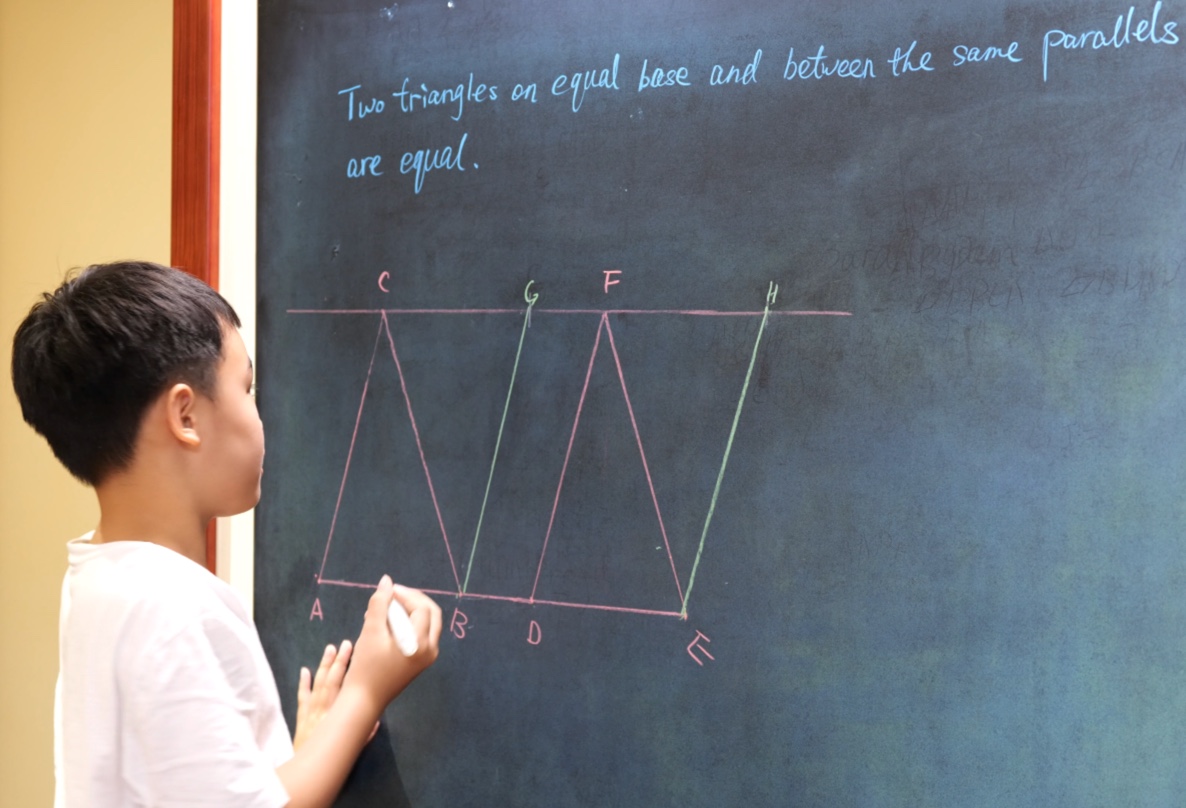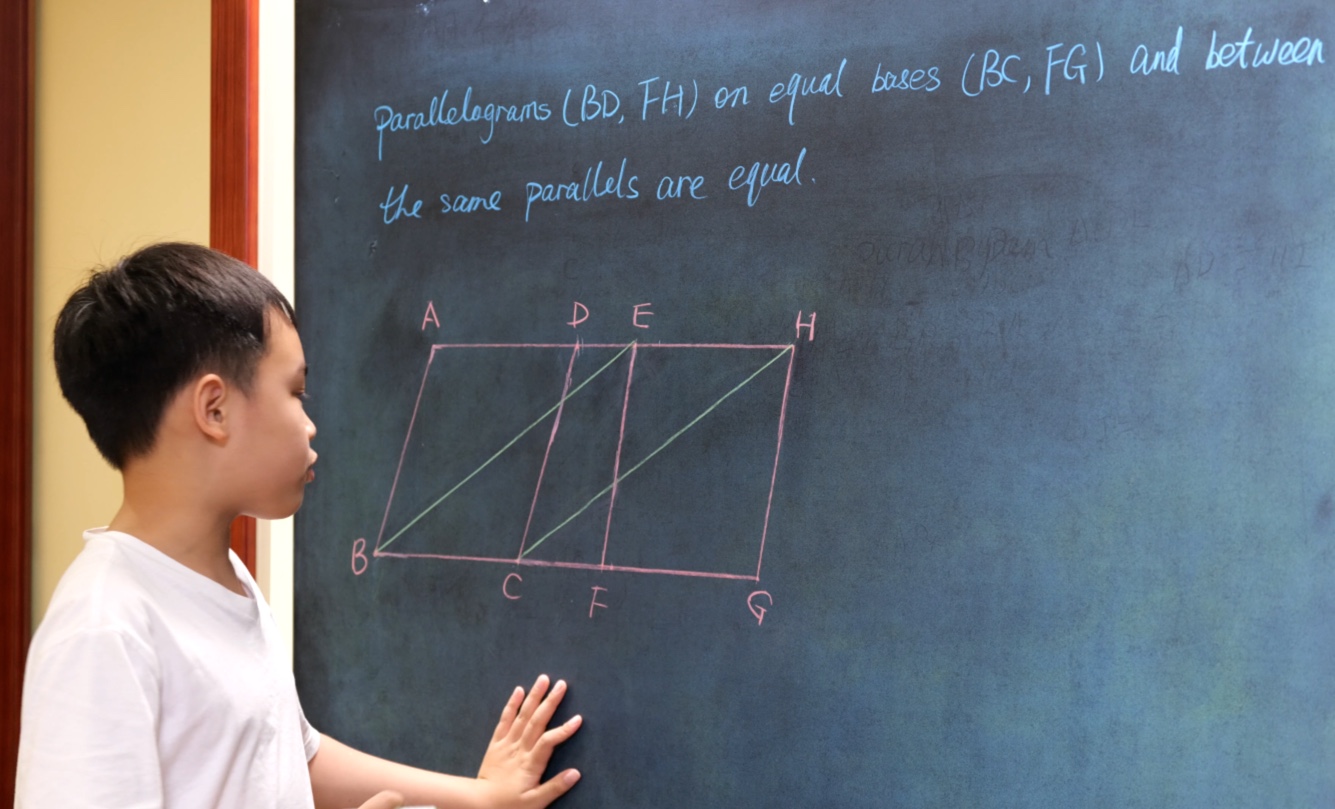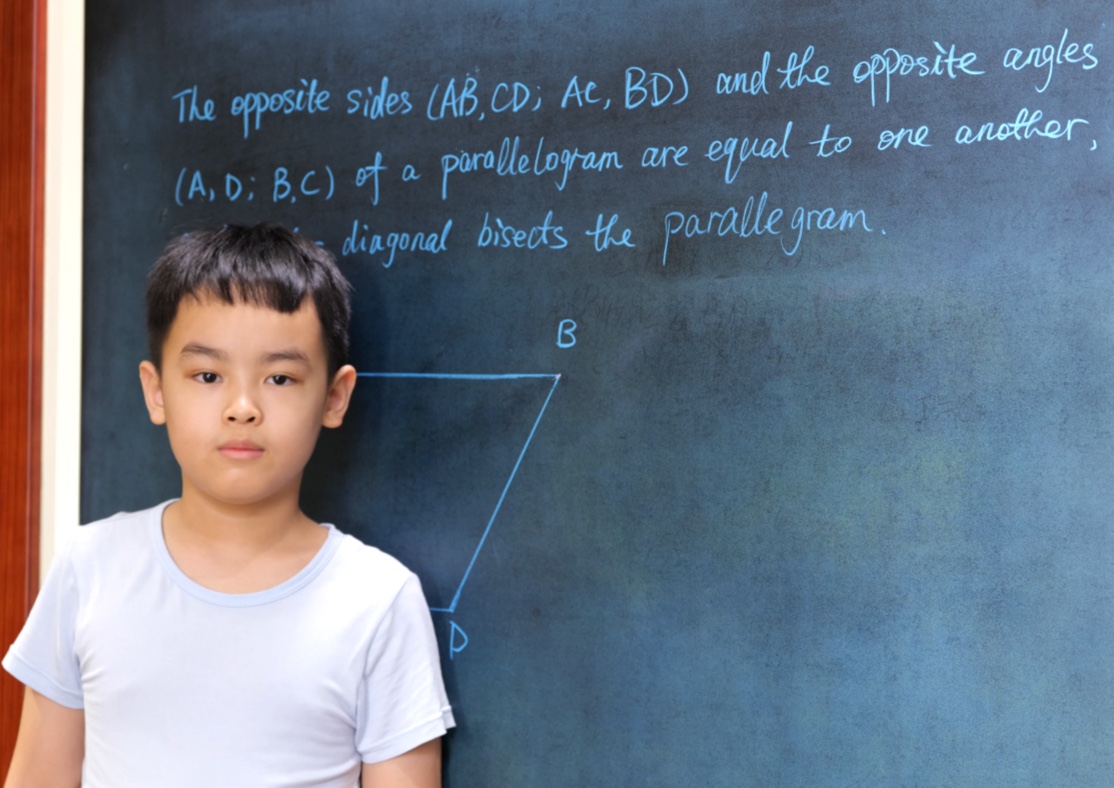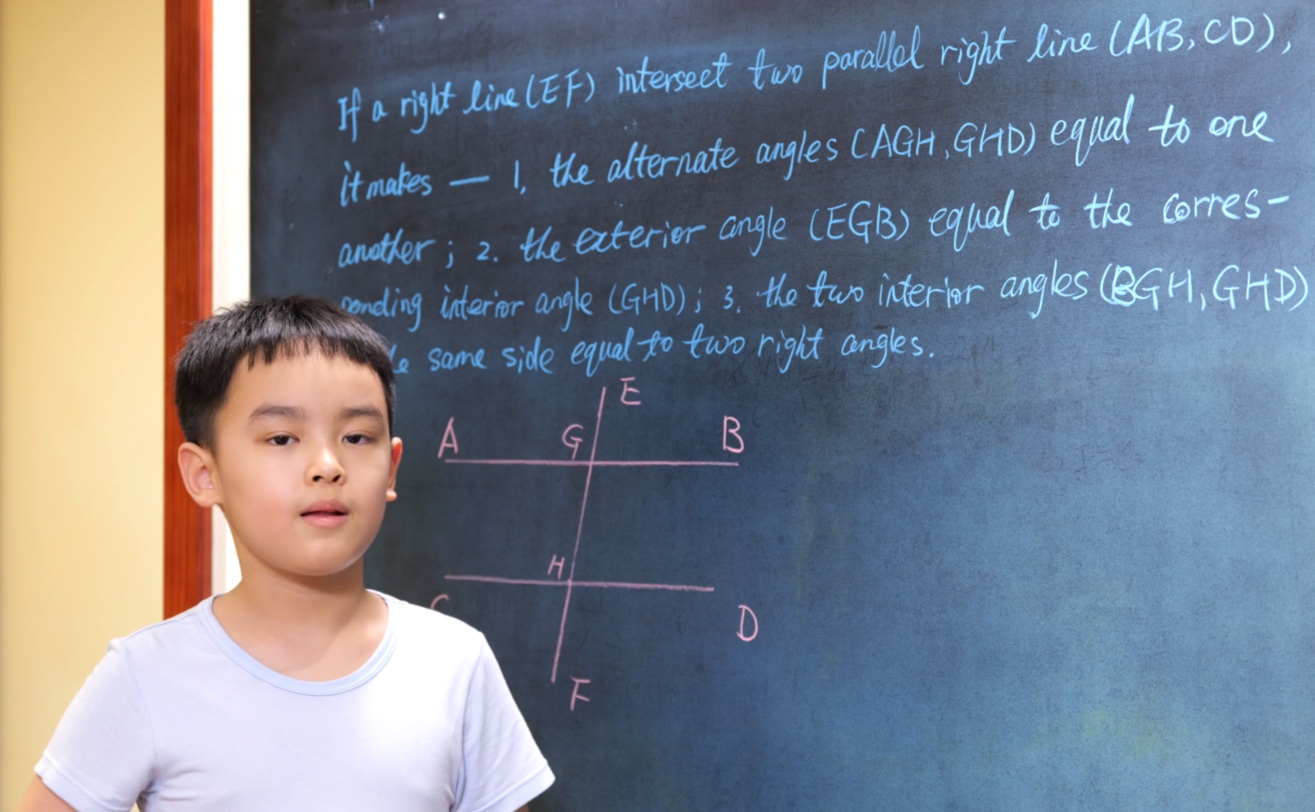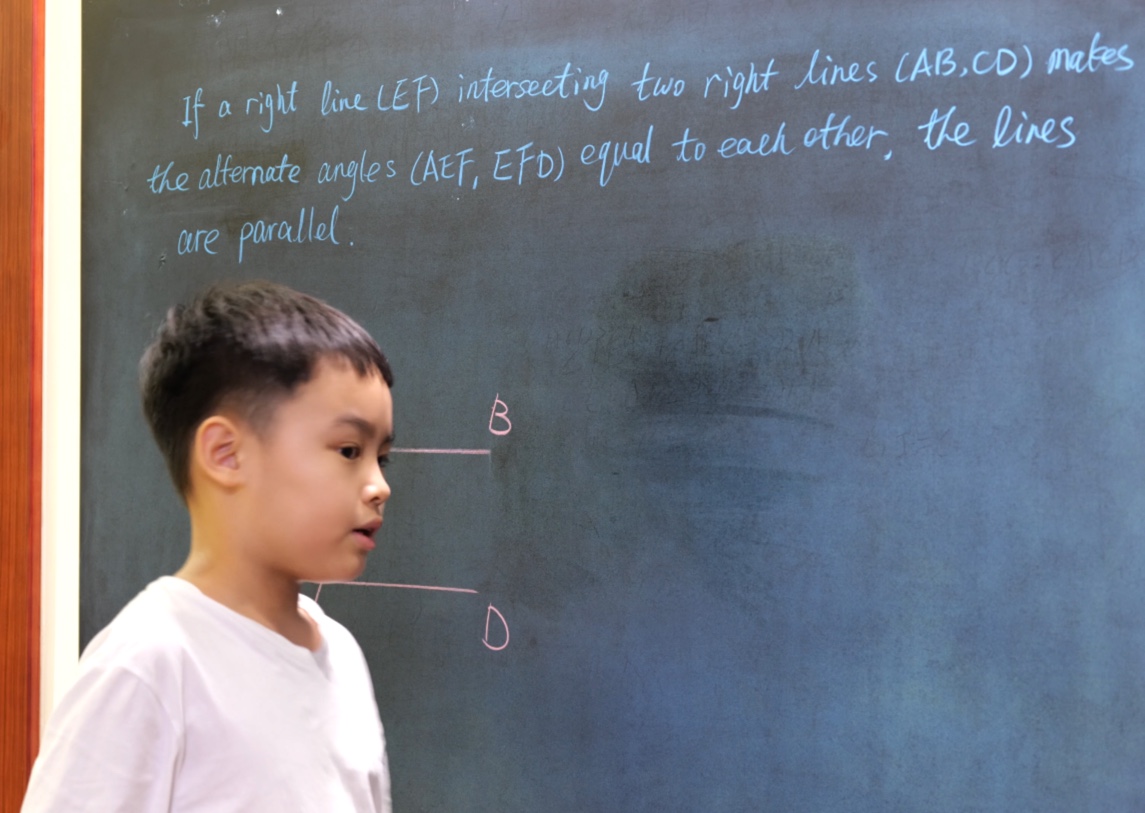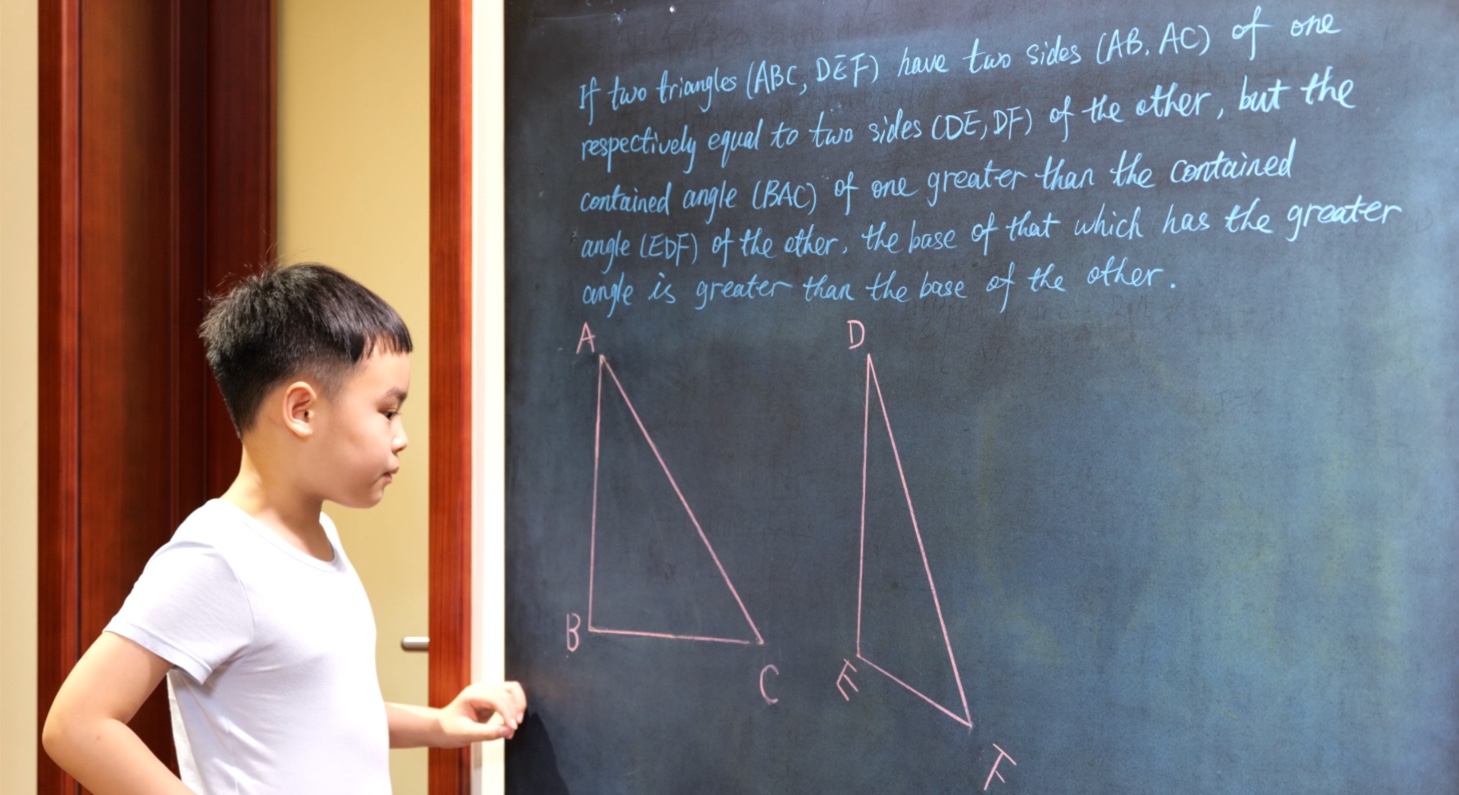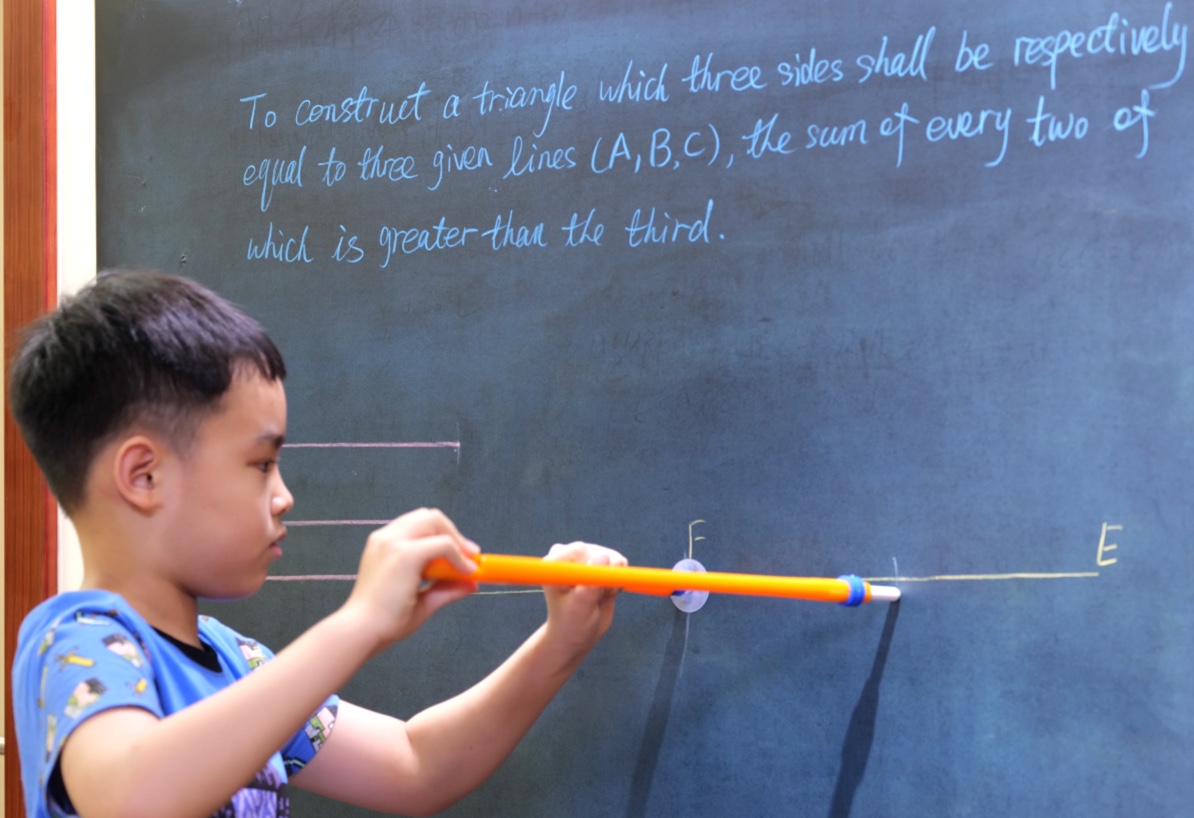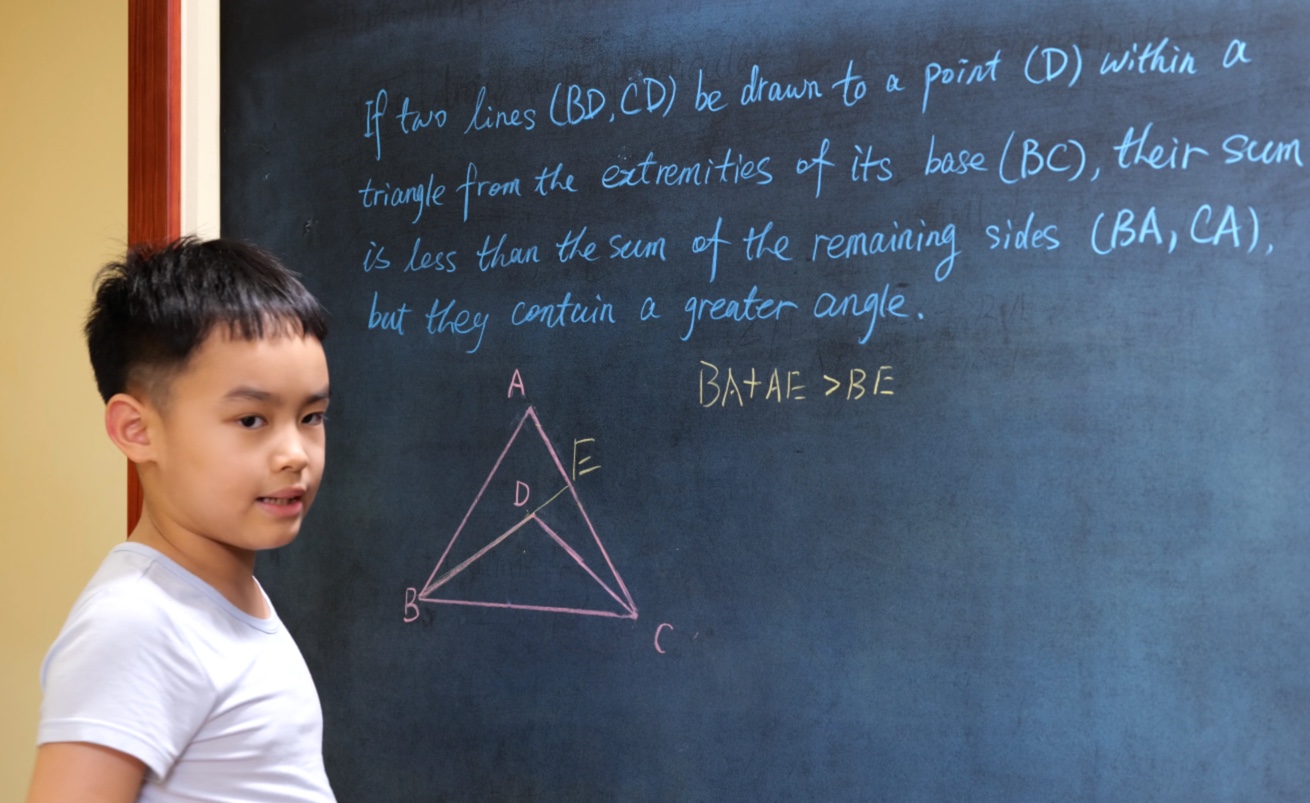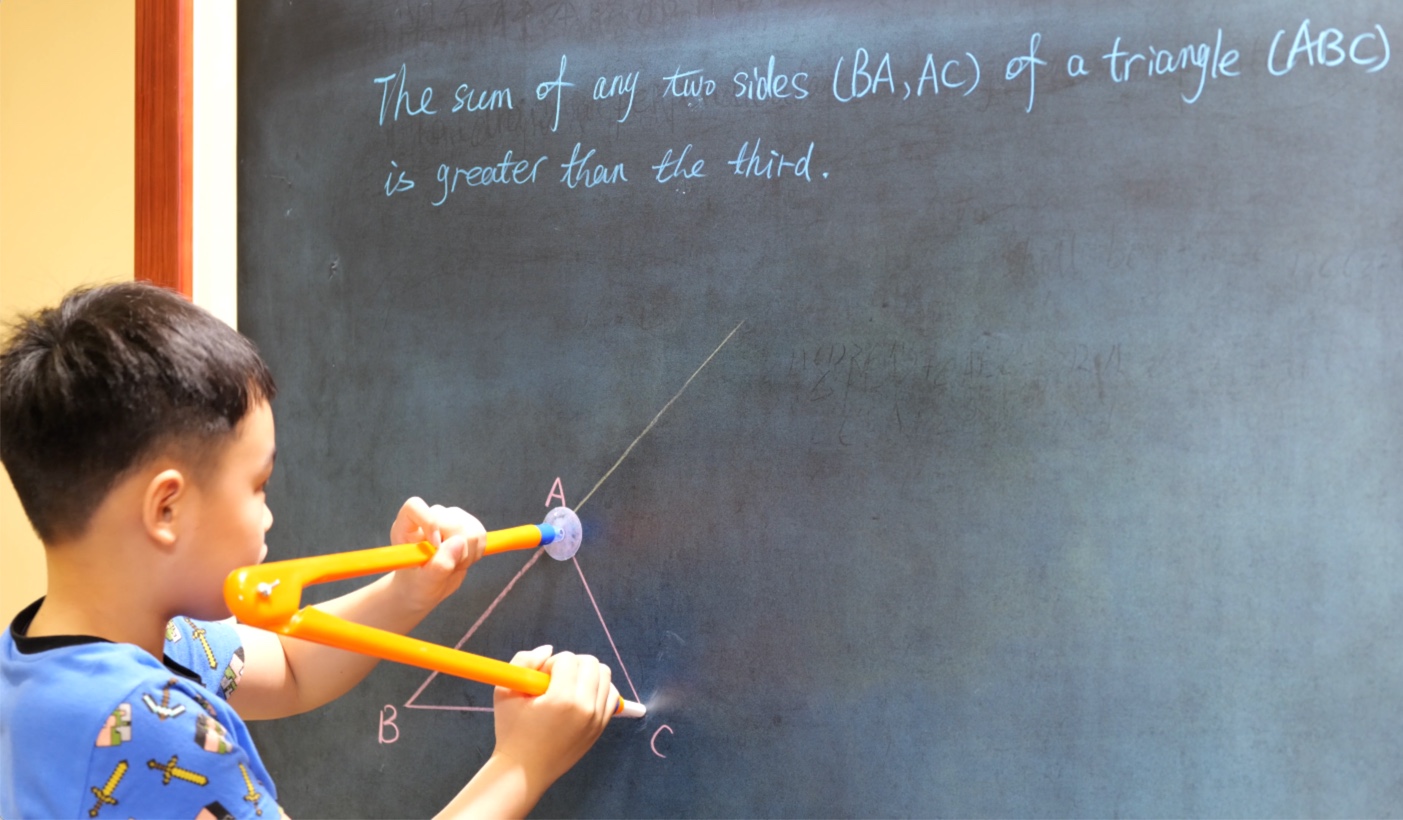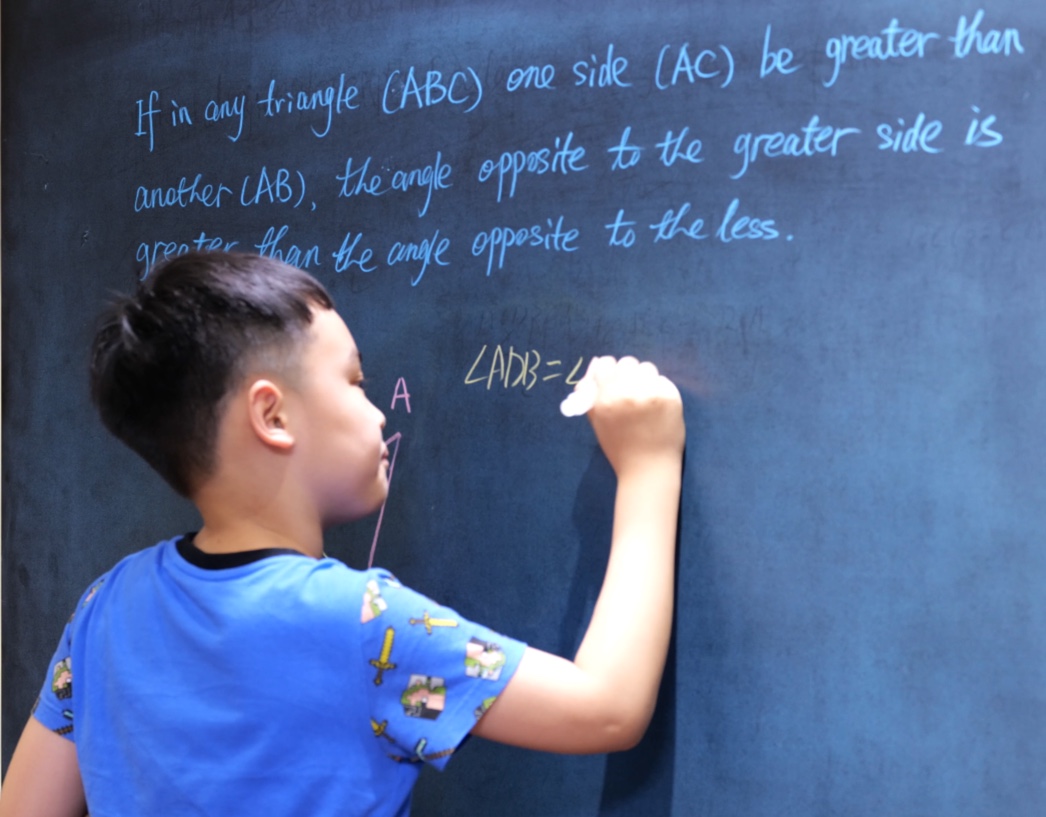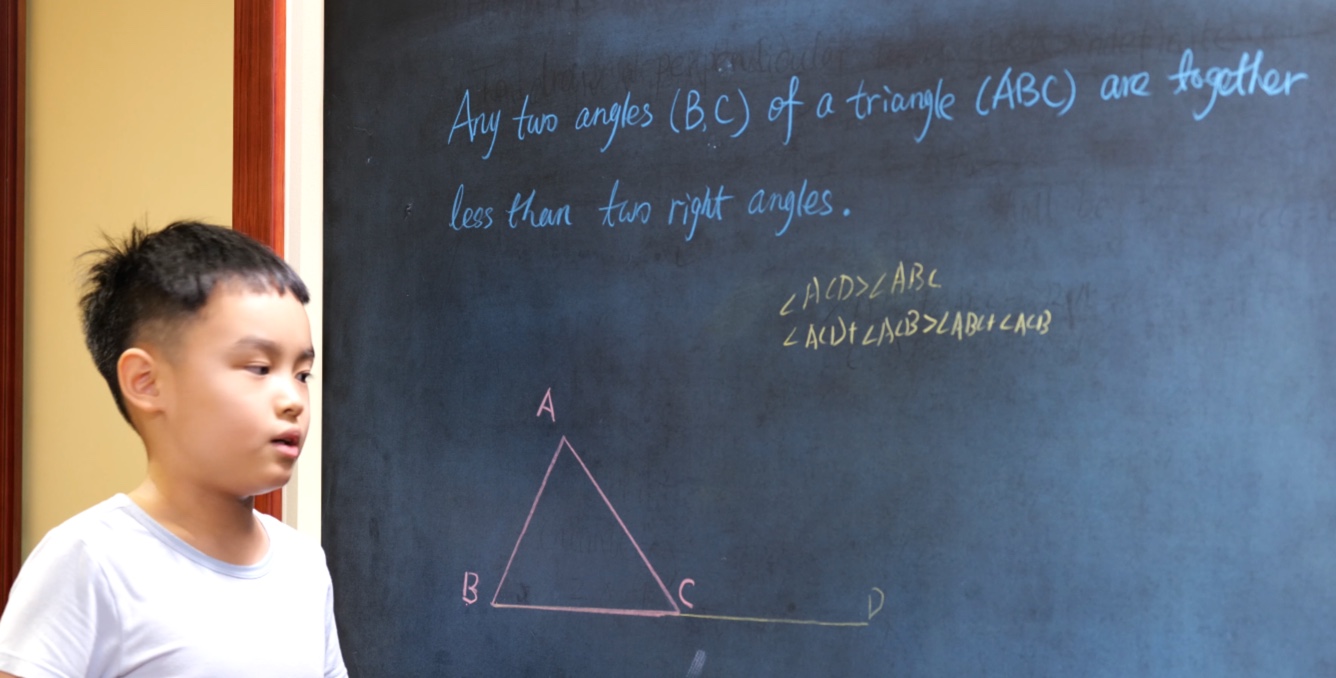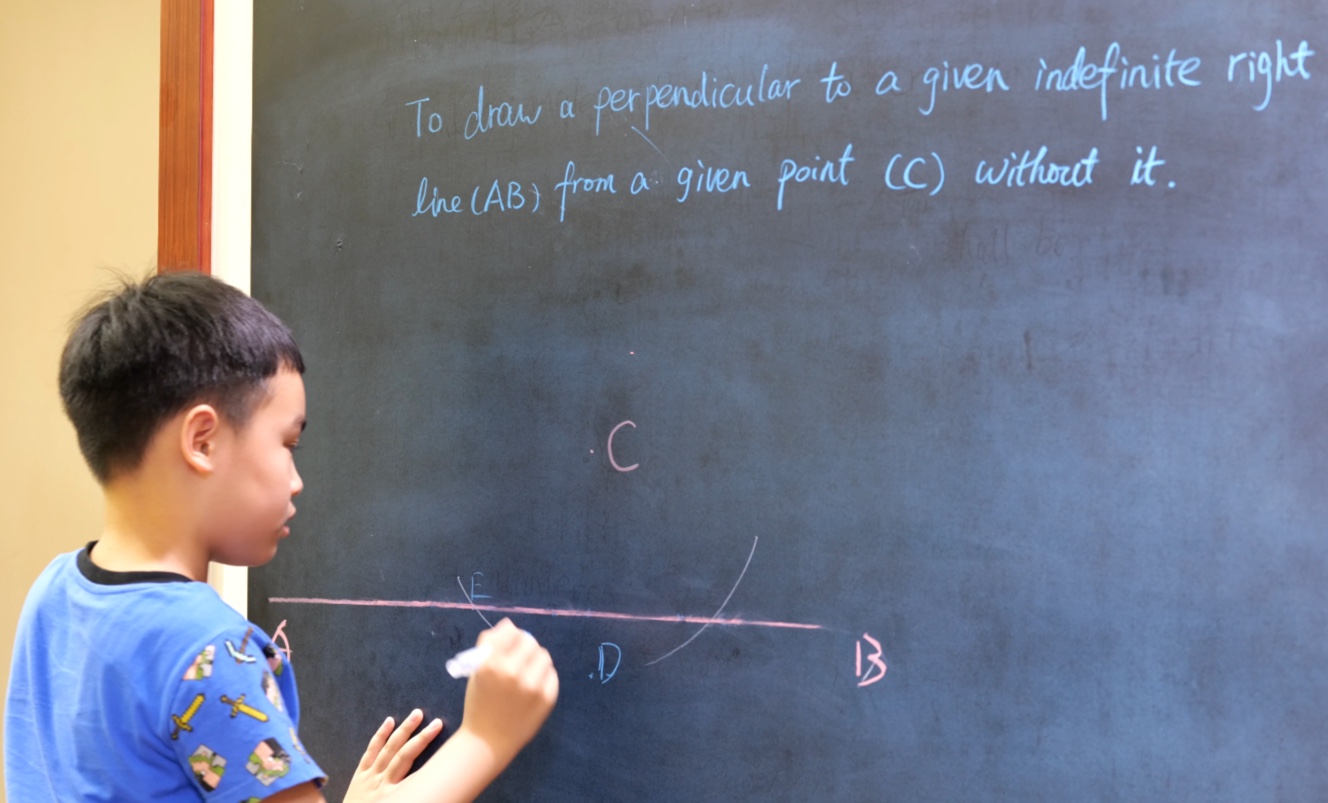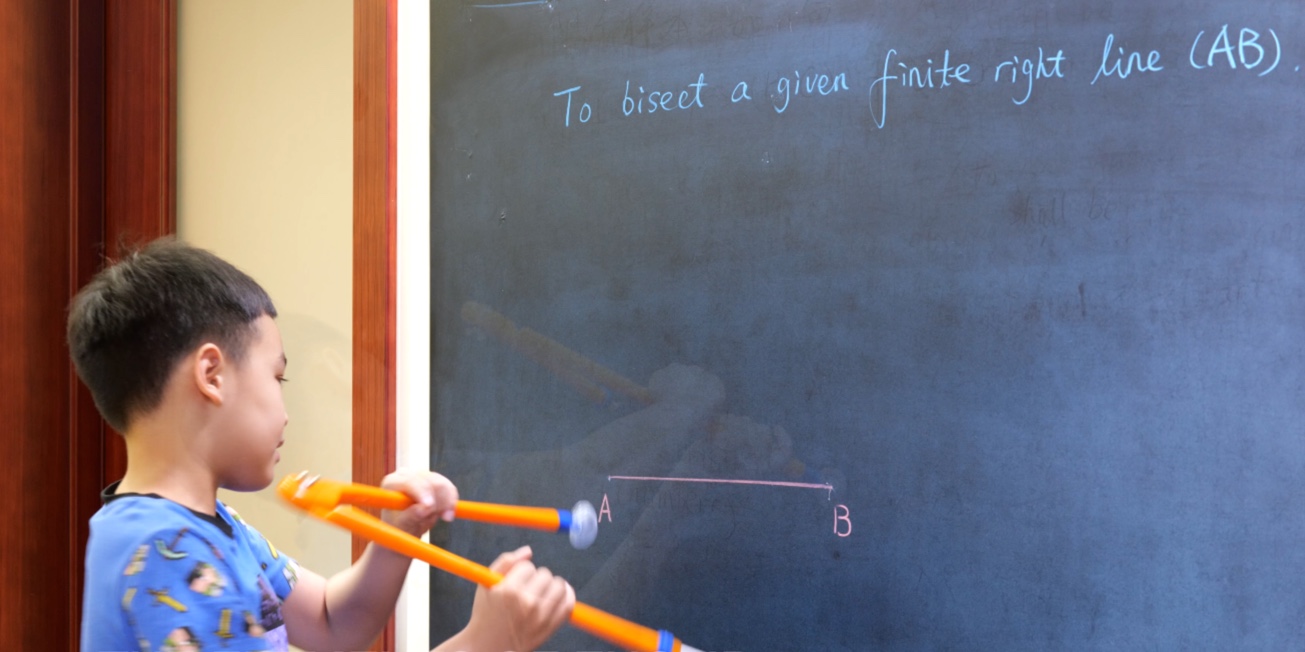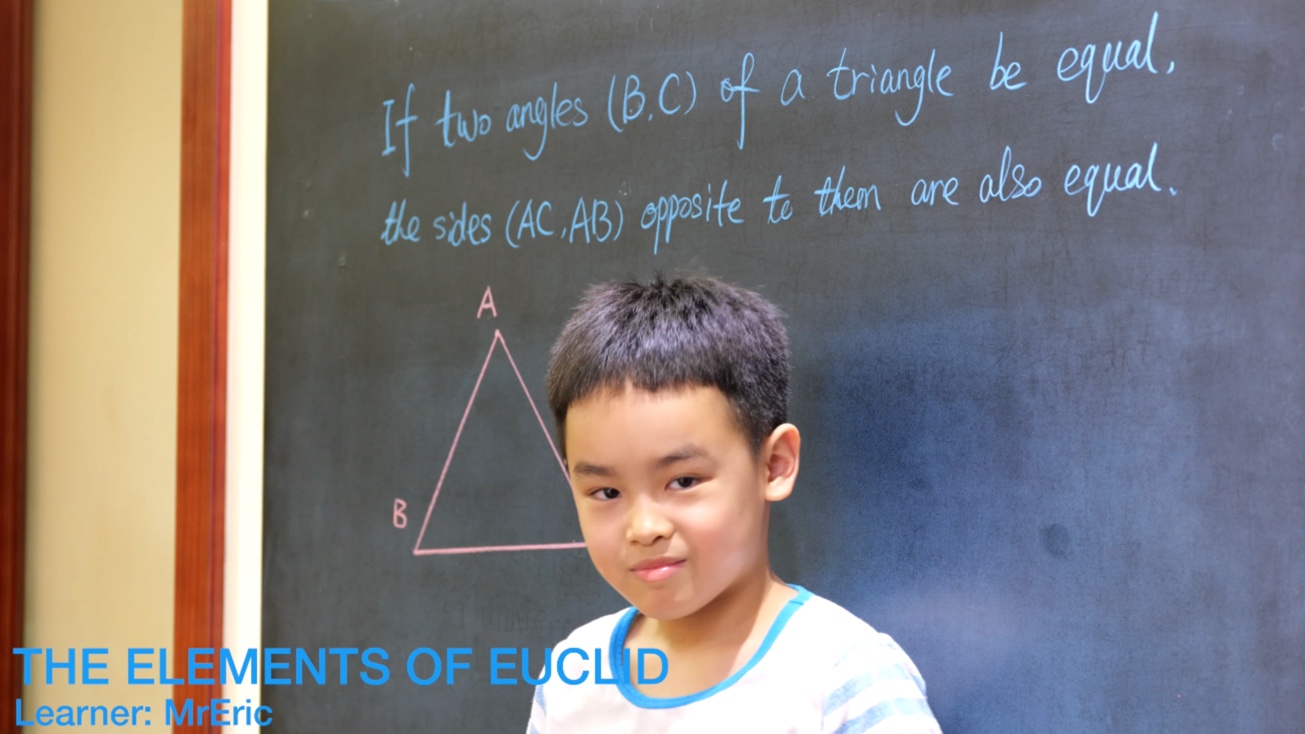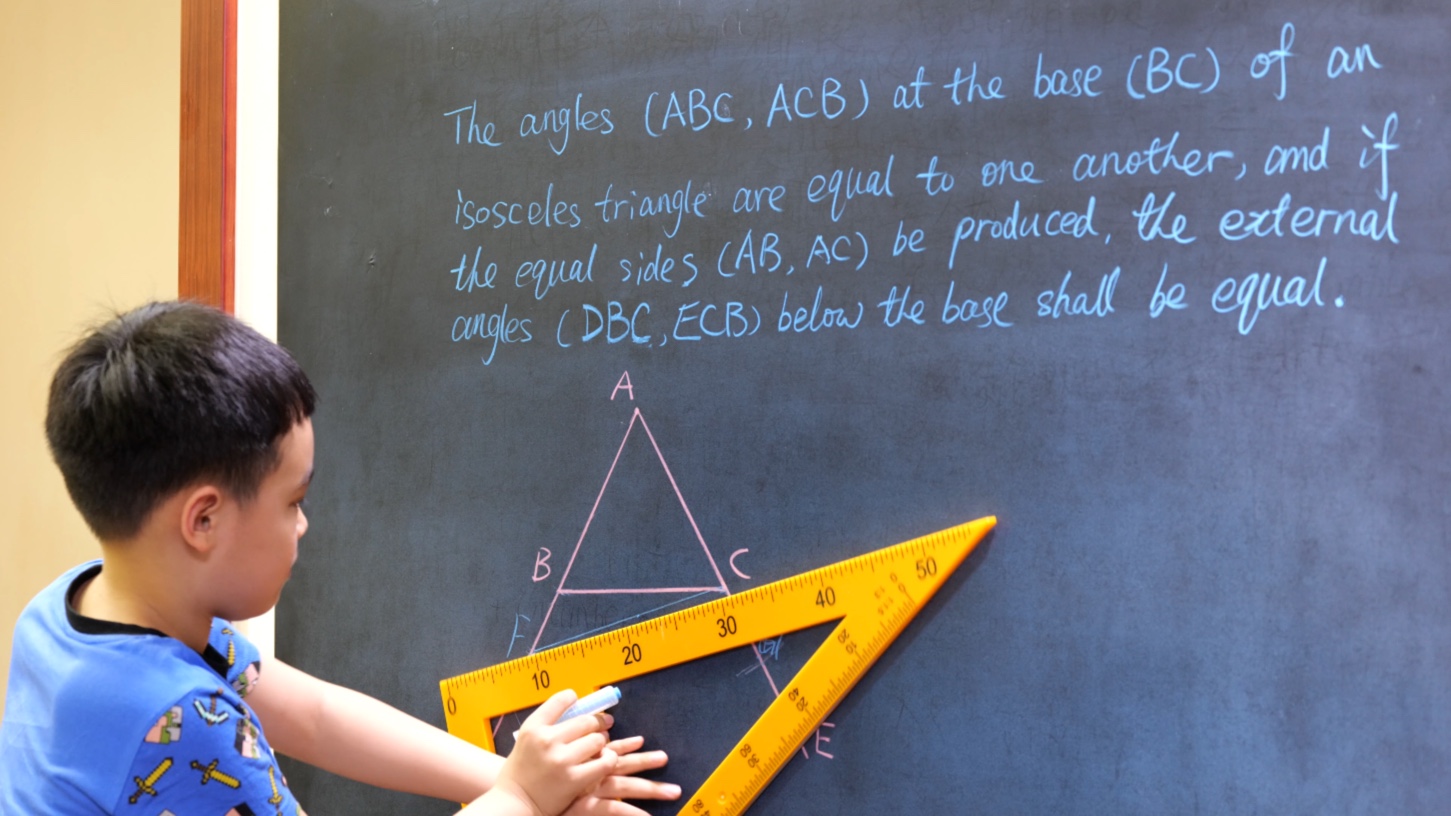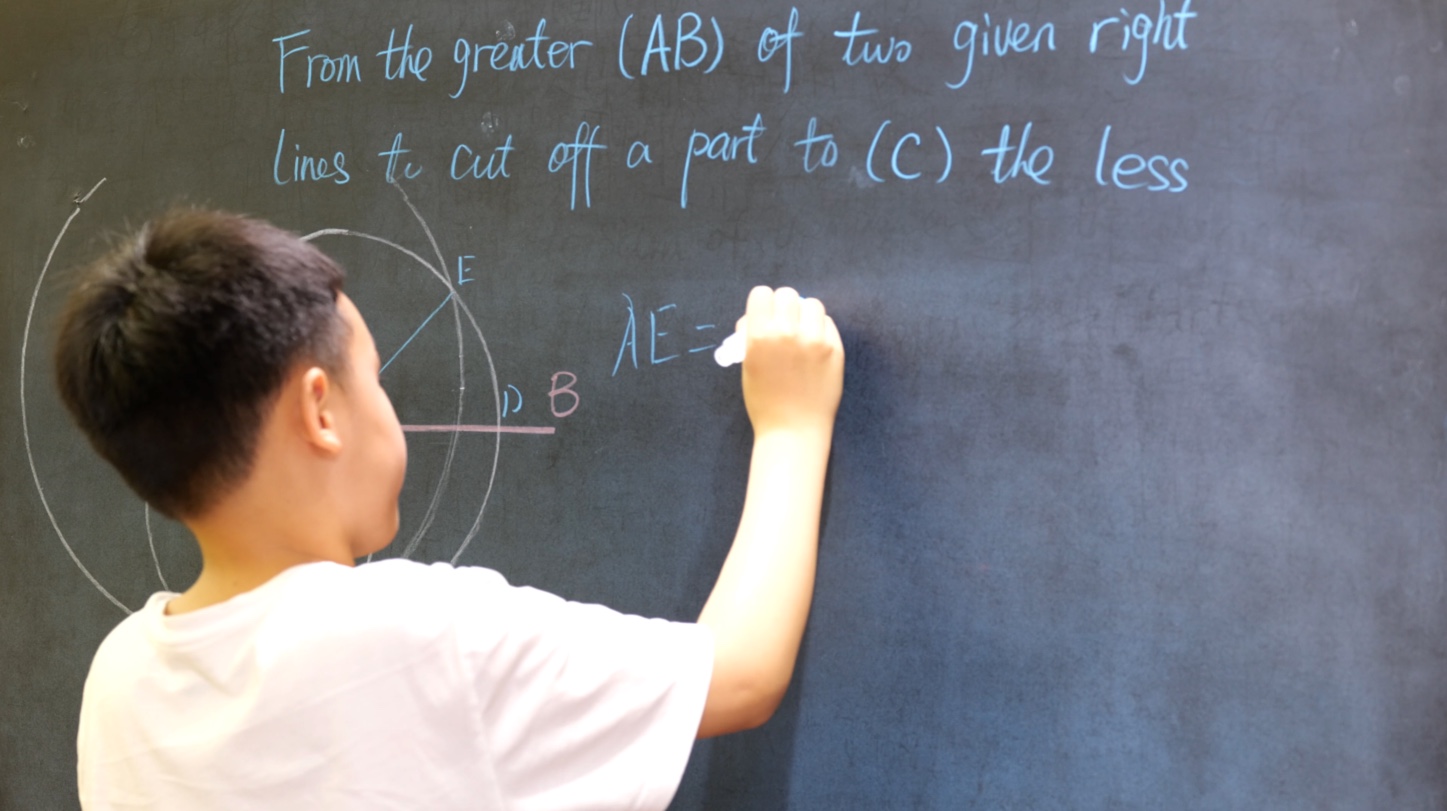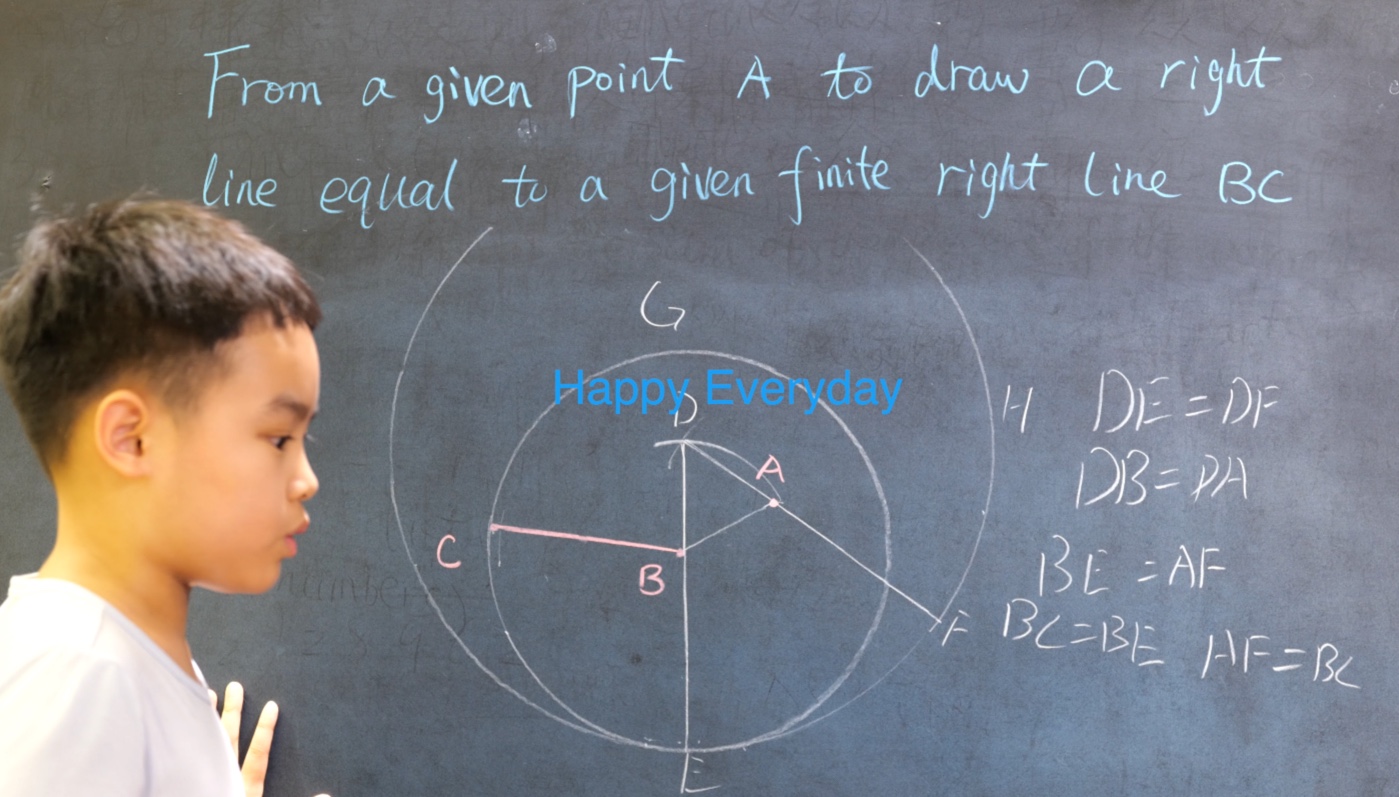Euclid Book II PROP. XIII. -- THEROREM.
In any triangle (ABC), the square on any side subtending an acute angle (C) is less than the sum of the squares on the sides containing that angle, by twice the rectangle (BC, CD) contained by either of them (BC) and the intercept (CD) between the acute angle and the foot of the perpendicular on it from the opposite angle.