Algebra Problem No.11
Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.
ALGEBRA
Algebra Problem No.9
Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.
Algebra Problem No.8
Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.
Algebra Problem No.7
Complete each problem below by hand. Show your work and provide a reason for each step. Calculators or other graphing devices are not allowed on this assignment.
Algebra Problem No.6
Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.
Algebra Problem No.5
Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.
Algebra Problem No.4
Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.
Algebra Problem No.3
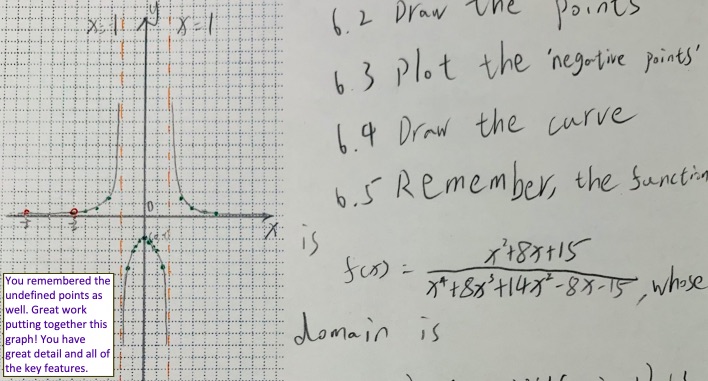
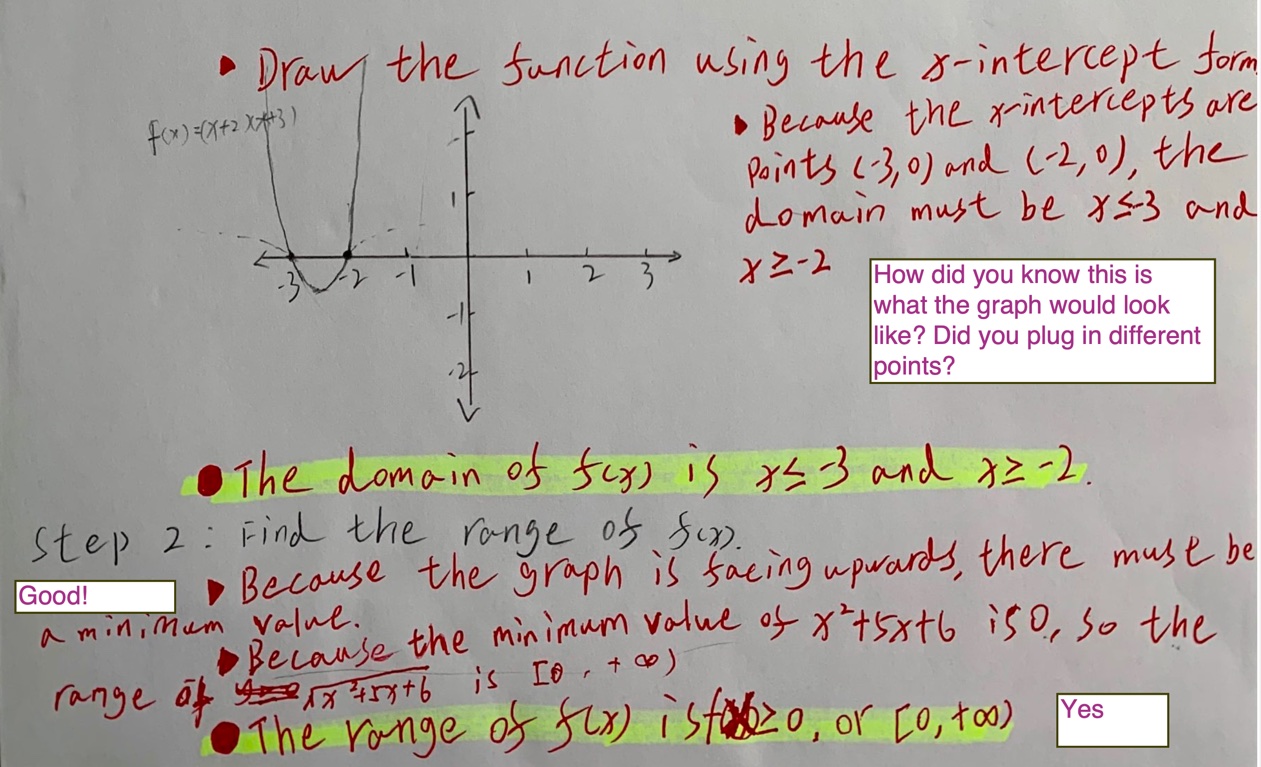
Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.
A very important value in mathematics is called the Golden Ratio. It appears in art and nature as well as architecture. This is because many believe this ratio creates the most beautiful proportions.
Algebra Problem No.2
Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.
Algebra Problem No.1
Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.
Free Question No.1
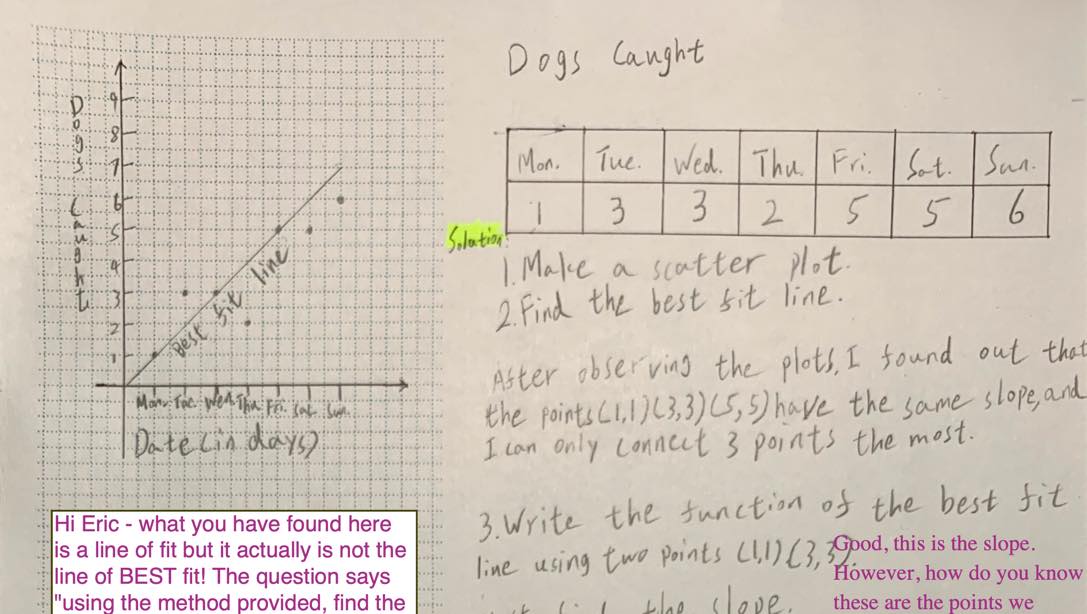
a. Assume that the length and width of a rectangle can be only whole numbers. How many rectangles of different dimensions have a perimeter of $12? \quad 14? \quad 16? \quad 18? \quad 24?$ (Orientation of the rectangle does not matter; that is, a $2 \times 3$ is the same rectangle as a $3 \times 2$.)
