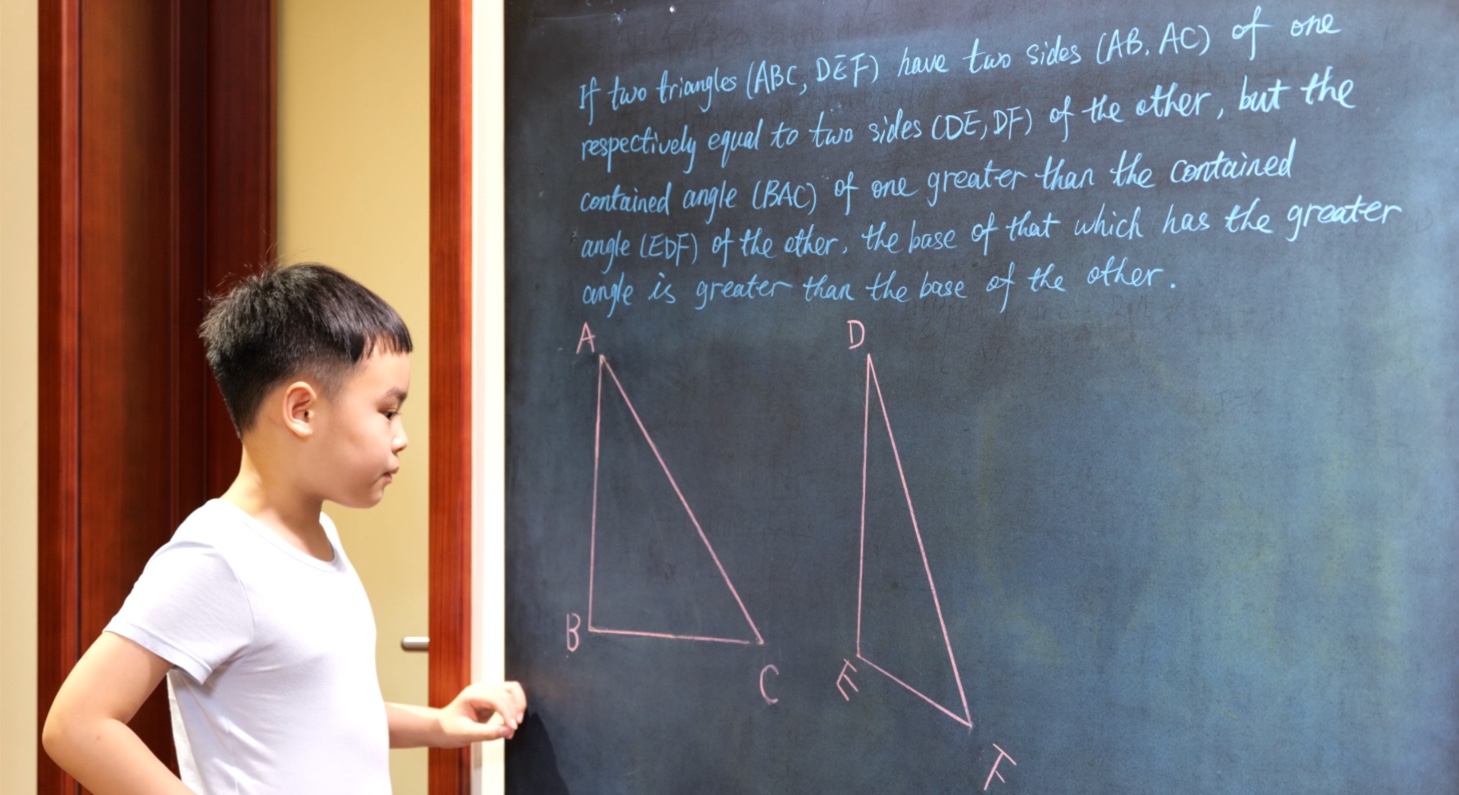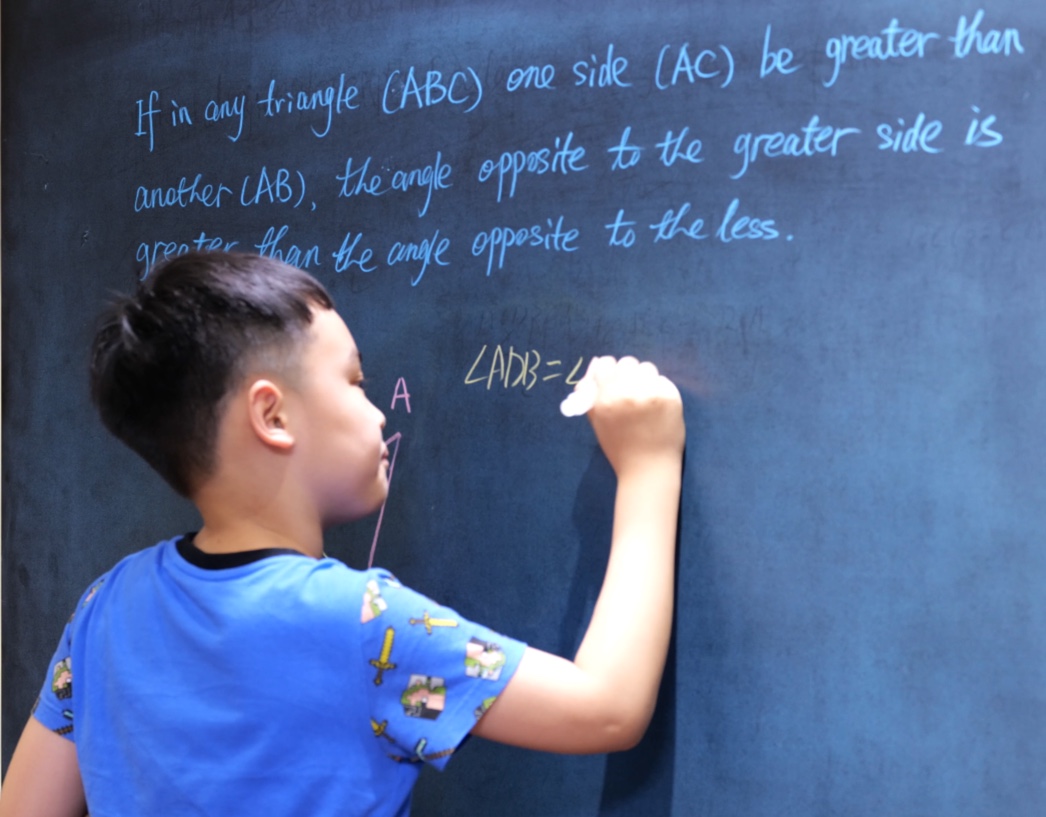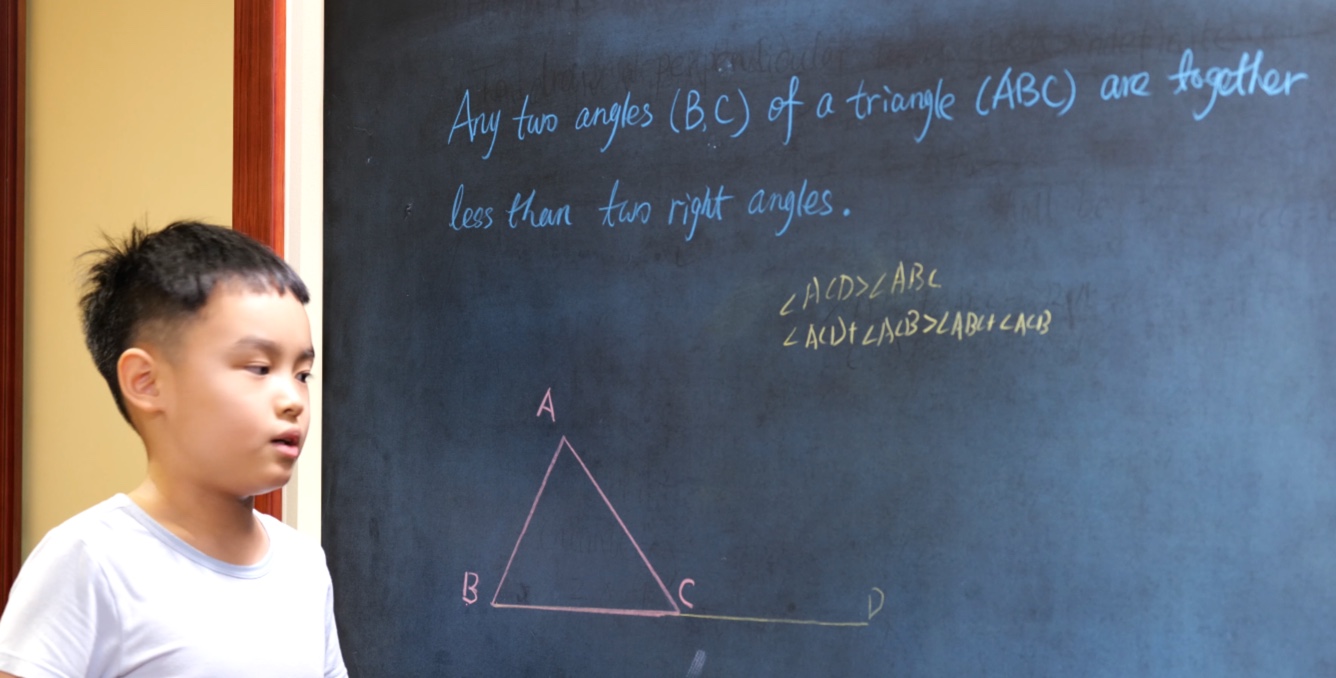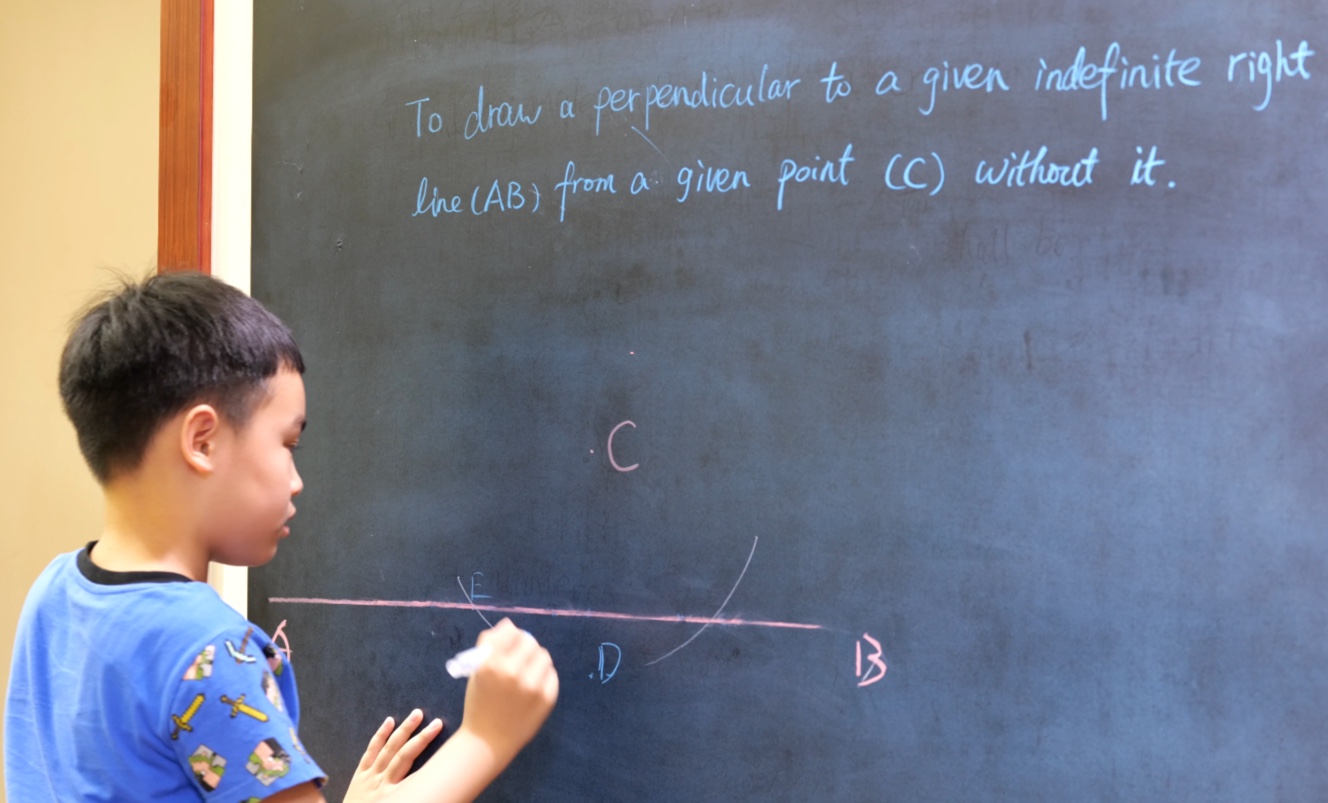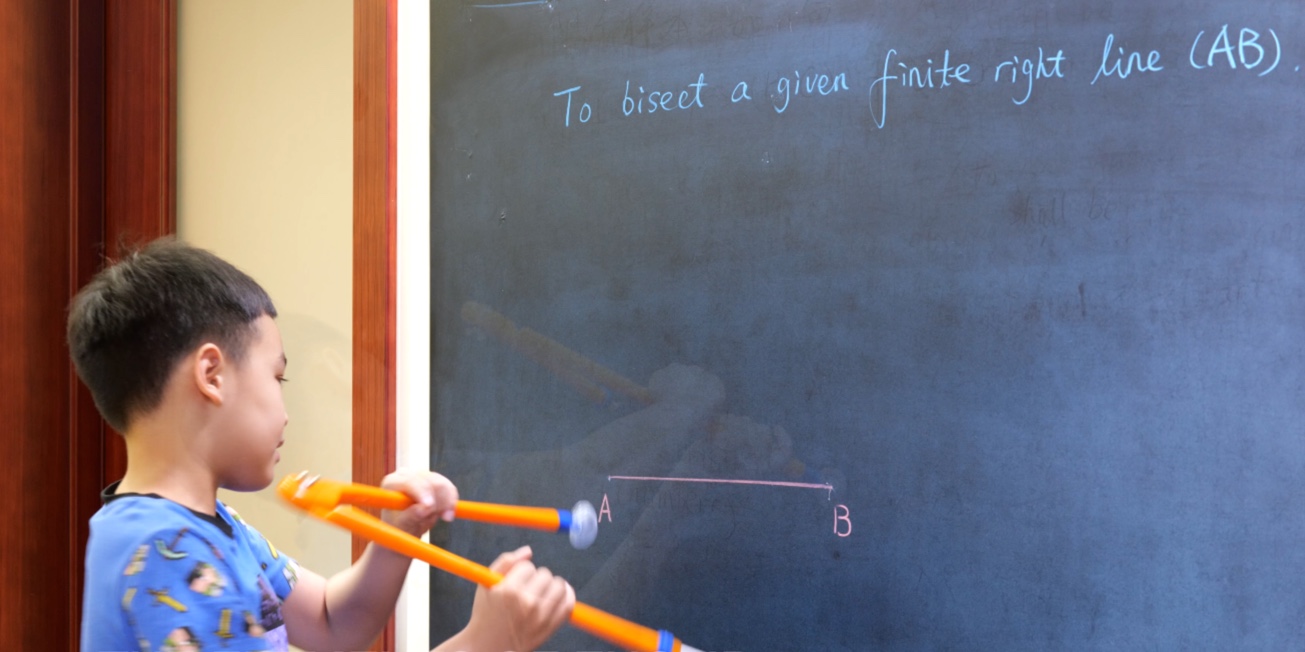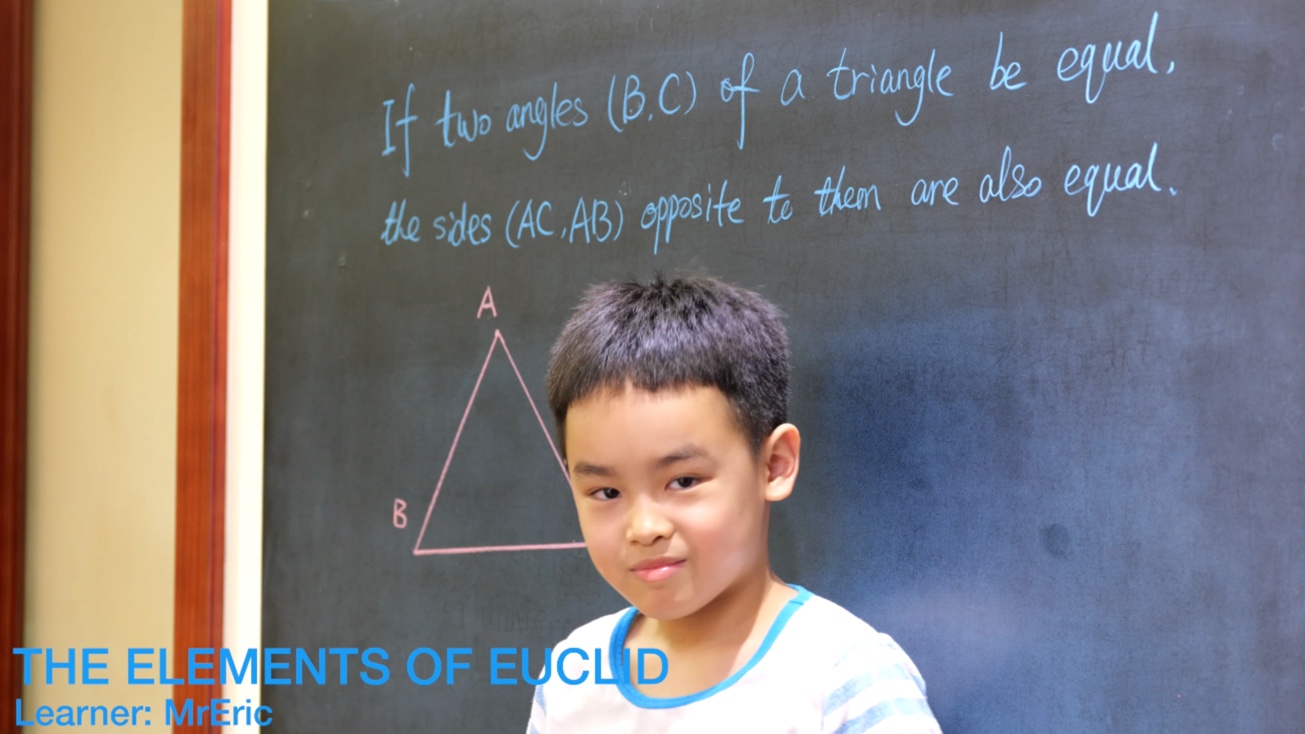Euclid Book I PROP. XXV. -- THEOREM.
If two triangles (ABC, DEF) have two sides (AB, AC) of one respectively equal to two sides (DE, DF) of the other, but the base (BC) of one greater than the base (EF) of the other, the angle (A) contained by the sides of that which has the greater base is greater them the angle (D) contained by the sides of the other.