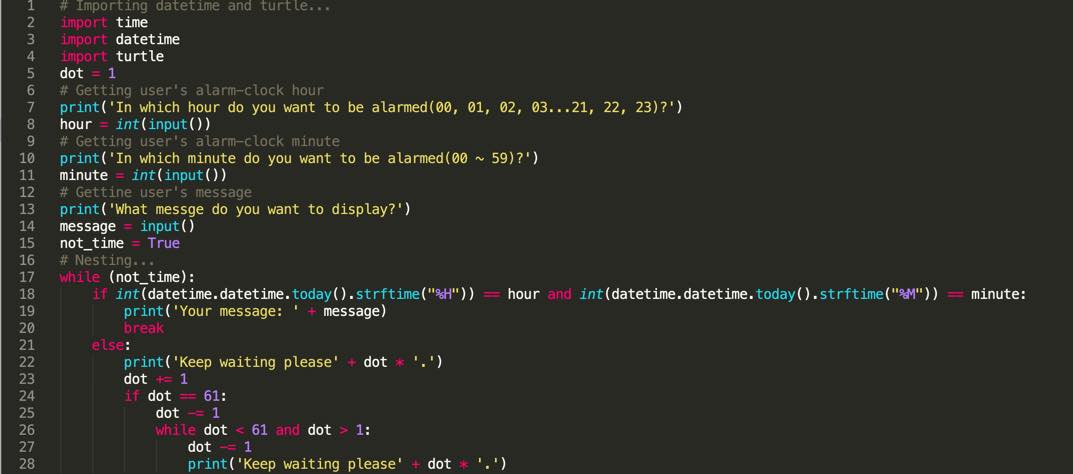
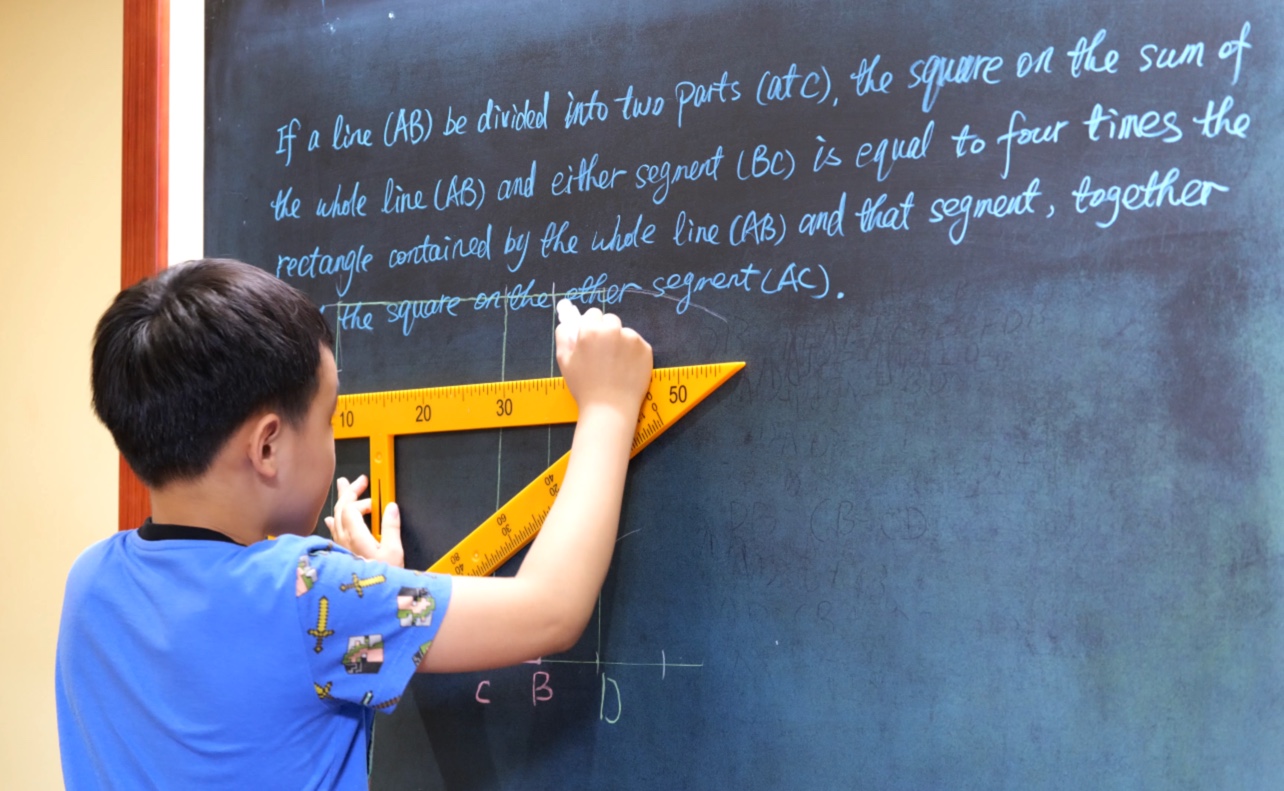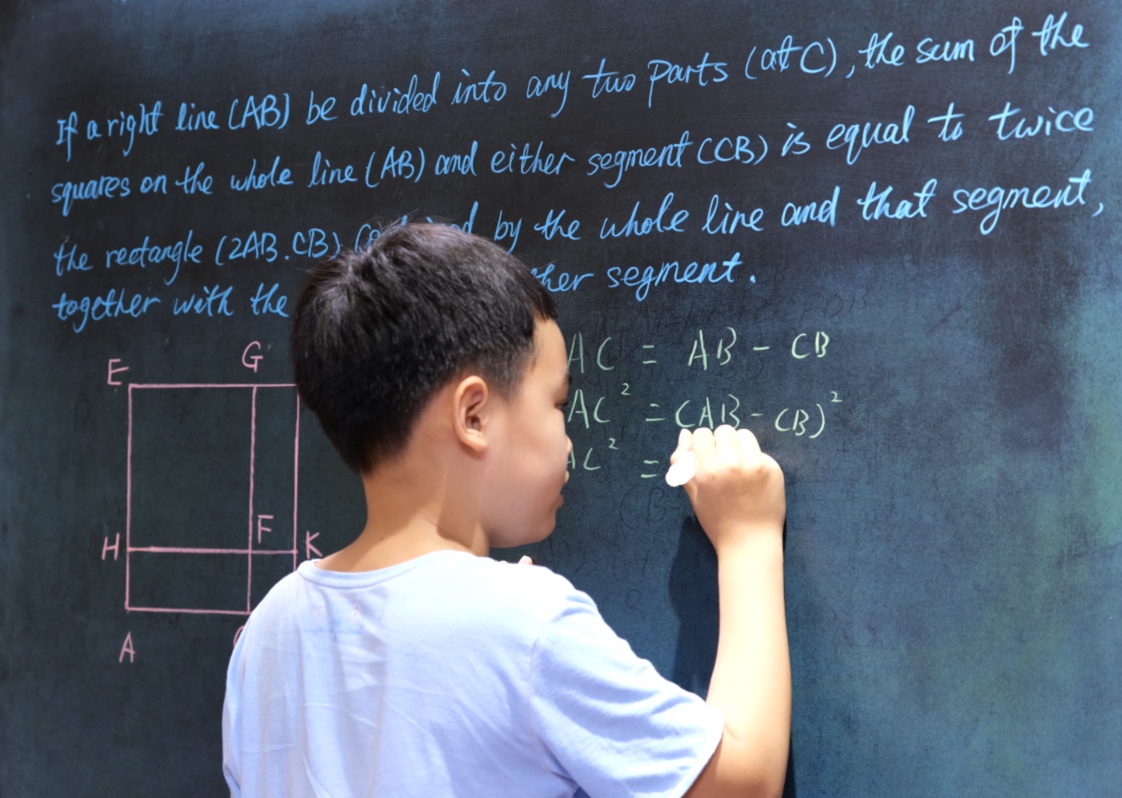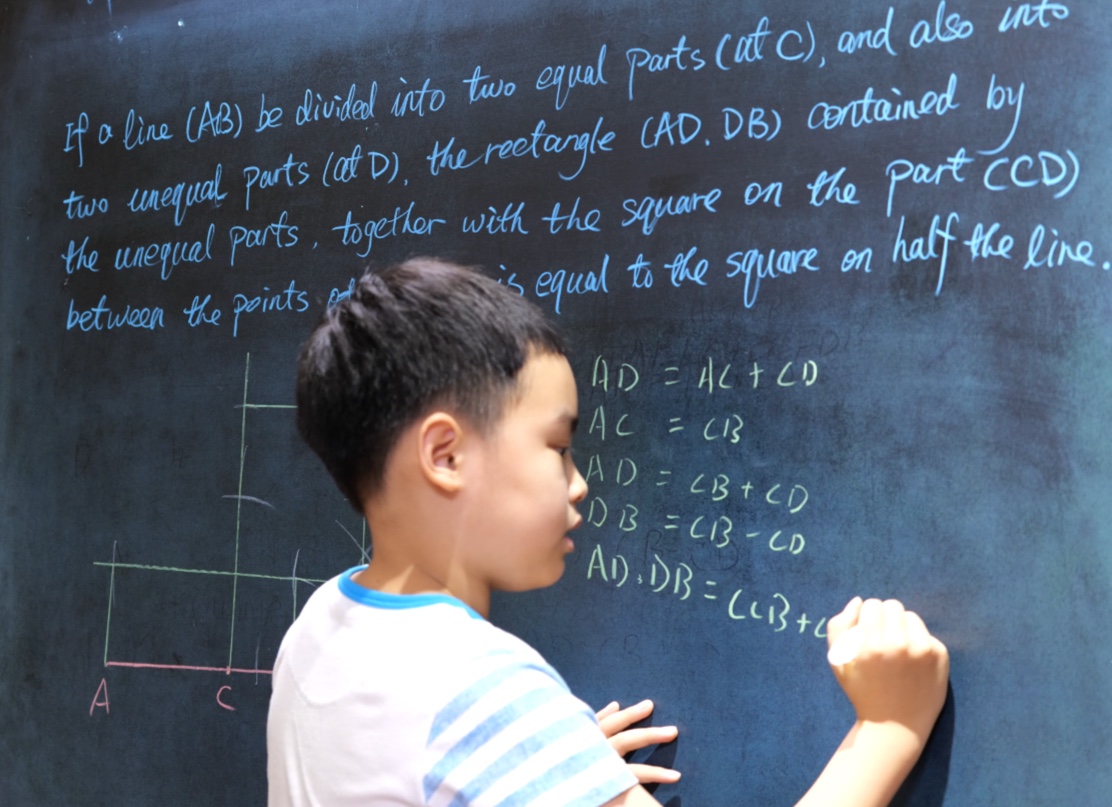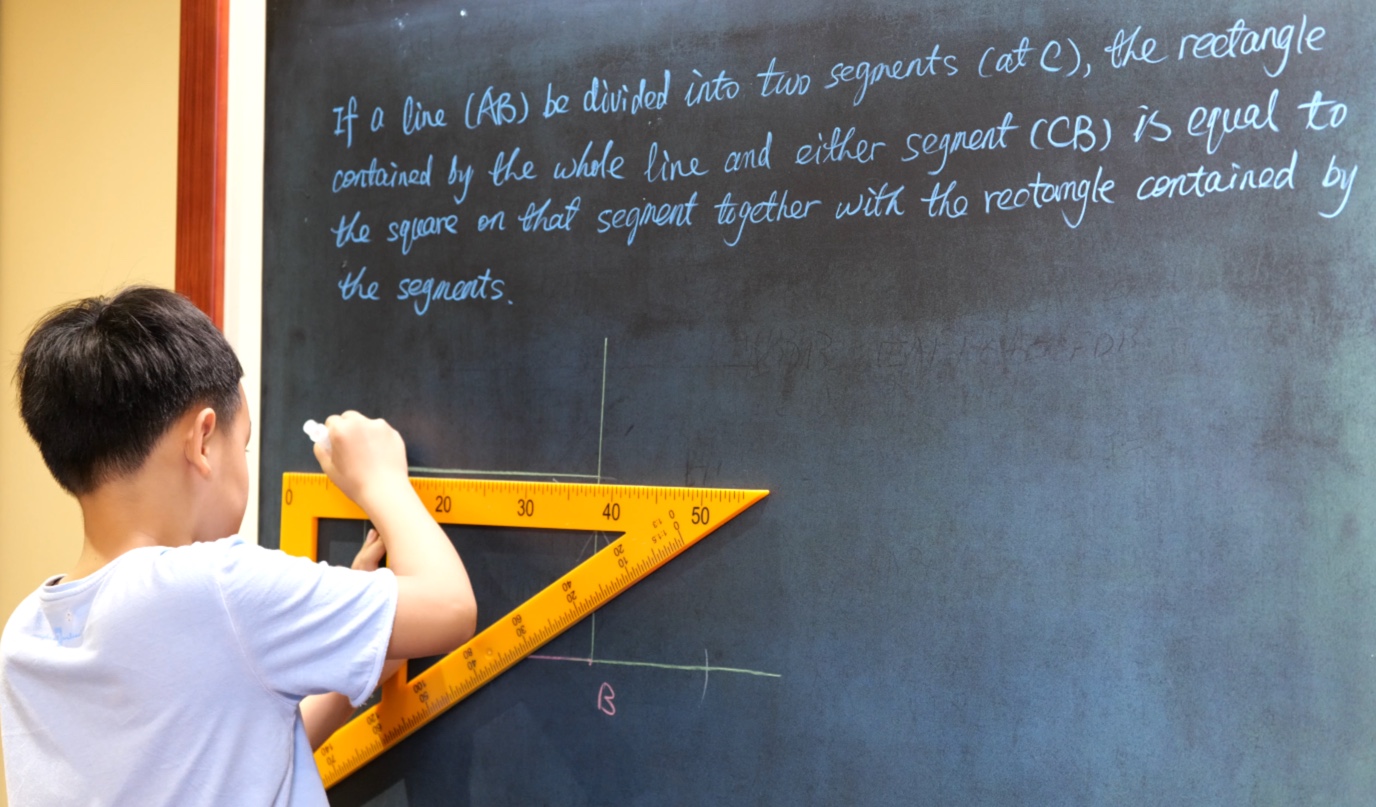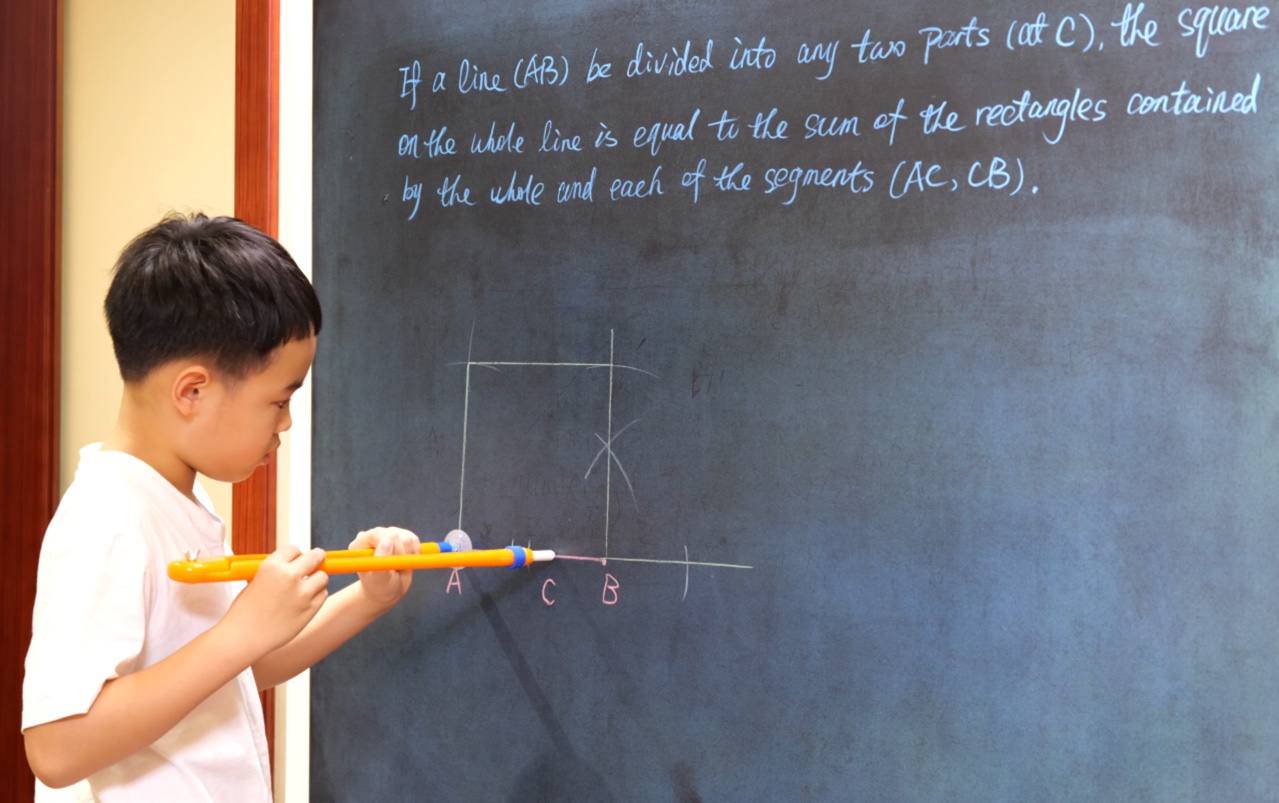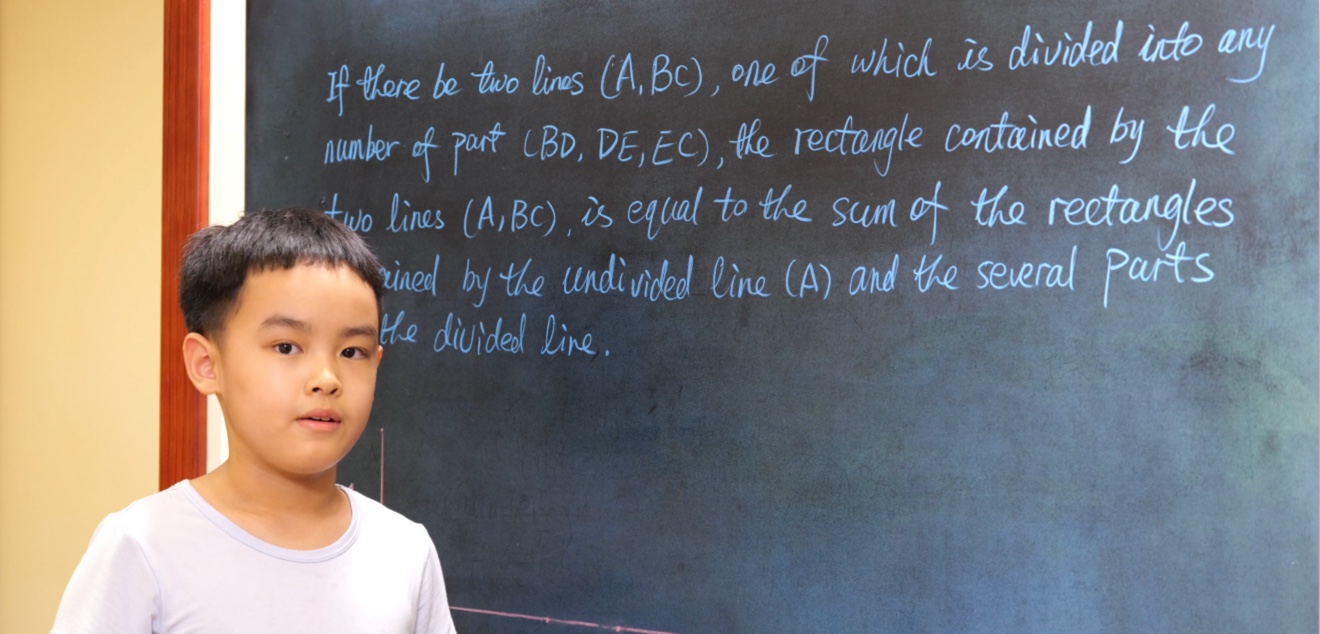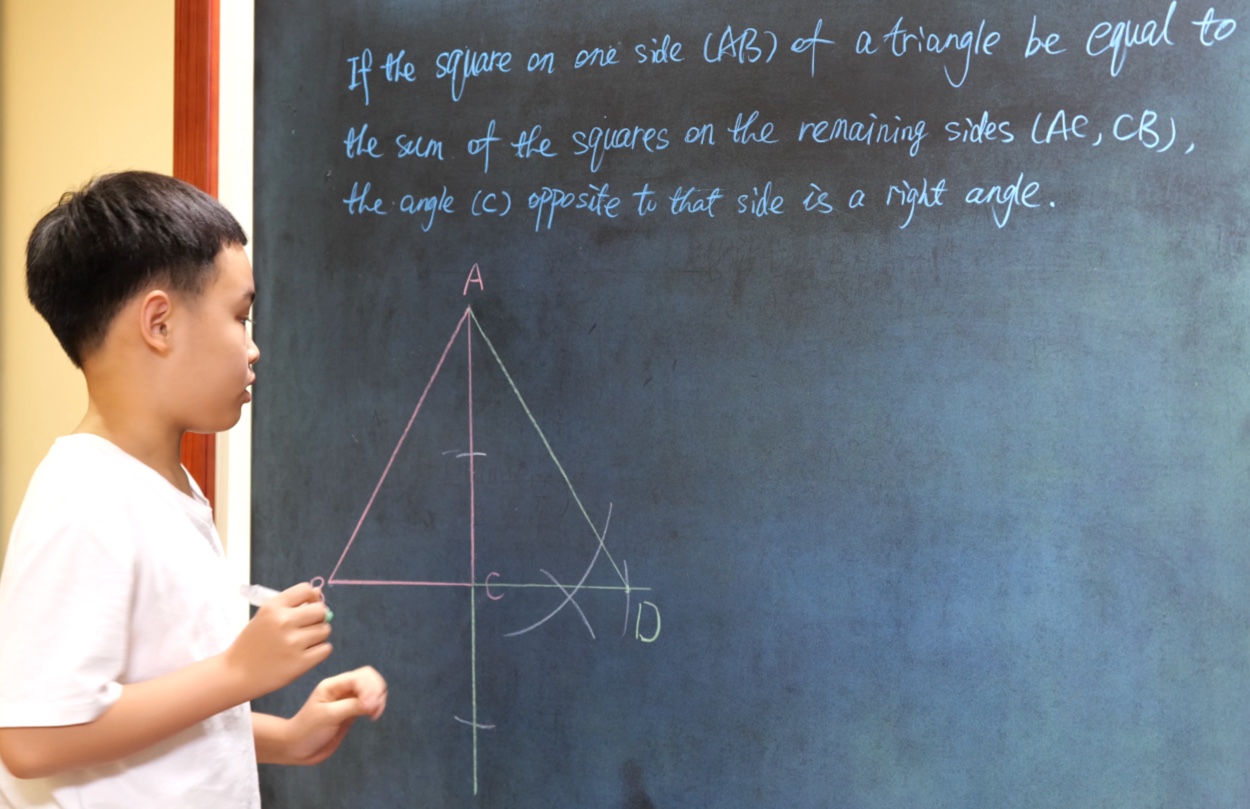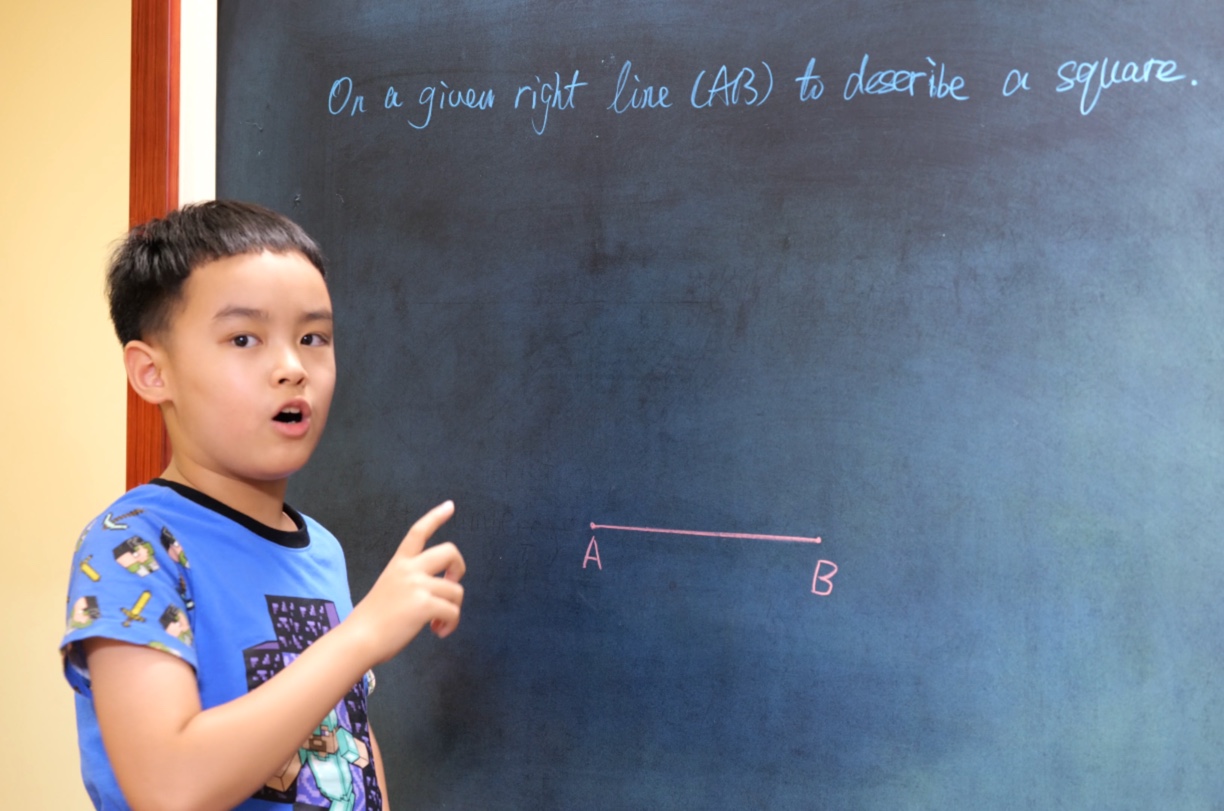Volunteer or not (G4)
Have you ever volunteered before? If you haven’t, then you should try your best to volunteer more. However, you don’t need to volunteer because everyone has their civil rights, which don’t force you to volunteer. Therefore you could not do it if you can’t, or don’t want to do it!