Complete each problem below by hand. Show your work and provide a reason for each step. Calculators or other graphing devices are not allowed on this assignment.
- Simplify the following complex fraction to linear factors. $$ \frac{\frac{6}{x^2+2x-15}-\frac{1}{x-3}}{\frac{1}{x+5}+1} $$ What are the key points of this function? When is this function positive?

Oops … missing question “When is this function positive”

- Solve the rational inquality $\frac{x^2-3x-2}{x^2+5x+6} \gt \frac{2-x}{x^2-4}$

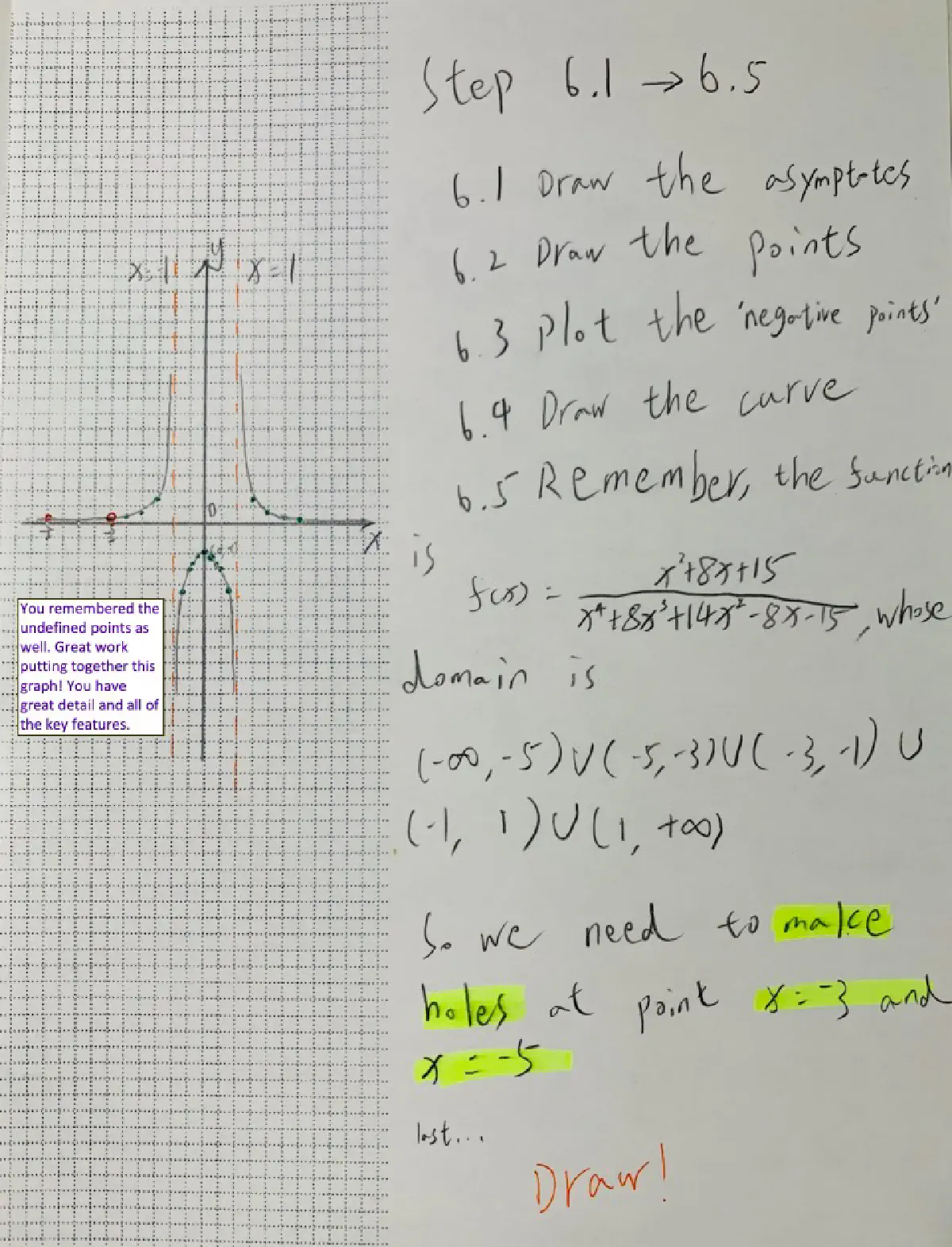
- Consider the rational function $$f(x)=\frac{x^2+8x+15}{x^4+8x^3+14x^2-8x-15}$$ Notice the denominator is the same as your work on Algebra Problem: Chapter 4. Use your previous results to:
a. Find all zeros of f(x).

b. Find the asymptotes.

c. Sketch a graph $f(x)$ including all key features previously found. Include how you graphed.