Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.
- Write a proof for the change of base formula. Remember, outside resources are not permitted and this should be $100%$ your own work. This formula can be proven using what you have learned in this course.

- Solve each of the following equations for $x$. Give specific reasoning for each step (not just listing a rule) and clearly conclude your solution.
a. $e^{ln(x^2−3)}=2x$

b. $e^{2x}−e^x−12=0$

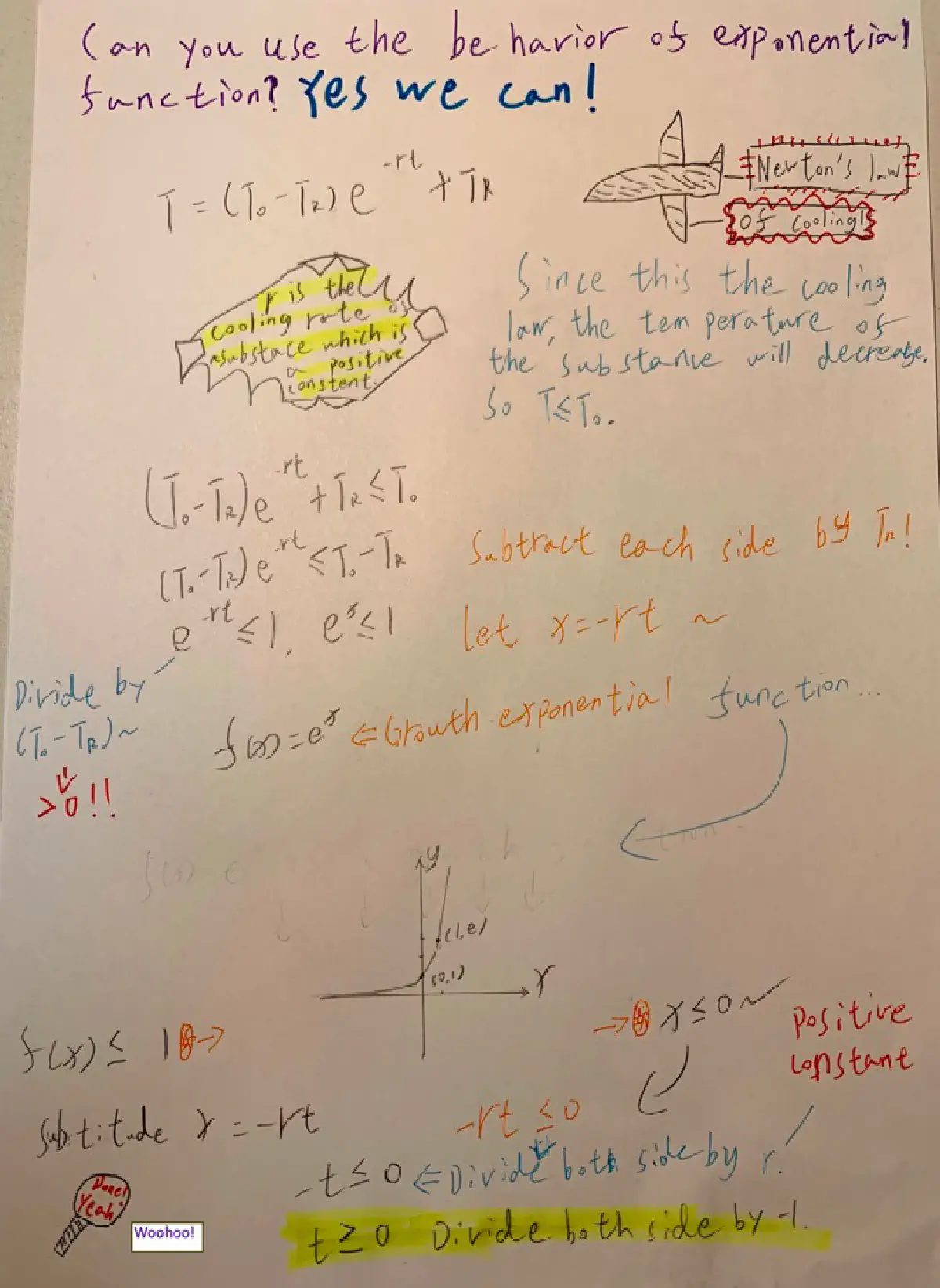
- A student has solved Newton’s Law of Cooling for time, $t$, and concludes the formula does not make sense as time is a negative value. Help the student to understand the formula. For simplicity, assume that $T_0>T_R$ and $T \ge TR$.
a. Solve Newton’s Law of Cooling $T=(T_0−T_R)e^{−rt}+T_R$ where $T_0$ is the initial temperature, $T$ is the temerature after $t$ minutes, and $T_R$ is the room temperature for time t.

b. Consider the value of $\frac{T−T_R}{T_0−T_R}$ and determine what are the possible values for this rational expression.

c. Explain to the student using the behavior of exponential/logarithmic functions why $t \ge 0$.